Soortelijke warmte

Inleiding

Op de middelbare school heb je vast al eens de soortelijke warmte van een materiaal bepaald. Je kunt een metalen blokje bijvoorbeeld verwarmen tot 100\(^{o}\)C en deze onderdompelen in een hoeveelheid water. Op basis van het bereikte temperatuurverschil kun je de soortelijke warmte van het materiaal bepalen. Echter, soortelijke warmte is een veel diversere eigenschappen dan het lijkt te zijn op basis van dit experiment. De soortelijke warmte van een stof hangt namelijk af van de temperatuur. In dit experiment bepaal je dan ook in een uitgebreider experiment de soortelijke warmte van koper.

Soortelijke warmte

Enkele begrippen uit de warmteleer

De warmtecapaciteit van een lichaam is de hoeveelheid warmte die nodig is om de temperatuur van het lichaam met een eenheid van temperatuur te verhogen. Die temperatuursverandering kan wel weer afhangen van de temperatuur van het lichaam zelf. De warmtecapaciteit bij temperatuur \(T_0\) is daarom gedefinieerd als een limietovergang:

()\[ C\left(T_{0}\right)=\left.\lim _{\Delta T \rightarrow 0} \frac{\Delta Q}{\Delta T}\right|_{T=T_{0}} \]

Hierin is \(\Delta Q\) de toegevoerde warmte en \(\Delta T\) de daardoor veroorzaakte temperatuurverandering. De warmtecapaciteit is doorgaans ook afhankelijk van de omstandigheid waaronder de warmte wordt toegevoerd: bij constant volume of bij constante druk. Voor vaste stoffen is het verschil tussen de warmtecapaciteit bij constant volume en bij constante druk zeer klein, zodat dit onderscheid hier niet van belang is. In deze proef zullen we daarom \(C\) blijven gebruiken voor de grootheid warmtecapaciteit, zonder aanduiding van de omstandigheid.

Uit de eerste hoofdwet van de thermodynamica (de totale hoeveelheid energie is constant) volgt dat onder bepaalde voorwaarden bij constant volume geldt: \(\Delta Q=\Delta U\), waarin \(U\) de inwendige energie van het lichaam is. Voor \(C(T_0)\) geldt dan:

()\[ C\left(T_{0}\right)=\left.\lim _{\Delta T \rightarrow 0} \frac{\Delta Q}{\Delta T}\right|_{T=T_{0}}=\left.\lim _{\Delta T \rightarrow 0} \frac{\Delta U}{\Delta T}\right|_{T=T_{0}}=\left.\frac{d U}{d T}\right|_{T=T_{0}} \]

Door meting van \(C\) krijgen we dus informatie over een belangrijke thermodynamische grootheid: de inwendige energie U. Bij meting van de warmtecapaciteit wordt de toegevoerde warmte overgedragen aan de interne vrijheidsgraden die bijdragen aan de inwendige energie, dit zijn bijvoorbeeld trillingen van de atomen of moleculen van de stof. Experimenteel bepaalde waardes van \(C\) kunnen vergeleken worden met diverse theorieën over de “inwendige energiestructuur” van de materie. Vandaar dat de warmtecapaciteit vaak gemeten wordt.

Om meetresultaten makkelijk te kunnen vergelijken, zowel onderling als met theoretische voorspellingen, geven we de gemeten warmtecapaciteit meestal per eenheid van massa of per eenheid van hoeveelheid stof (d.w.z. per kg of per mol). De waarde hangt dan niet langer af van het gebruikte lichaam, maar alleen nog van de stof. De aanduiding hiervoor is soortelijke warmte of specifieke warmte, waarbij dan nog in het midden is gelaten of deze per kg of per mol bedoeld wordt, met de corresponderende eenheden kJkg\(^{-1}\)K\(^{-1}\) en kJkmol\(^{-1}\)K\(^{-1}\), respectievelijk. Voor deze grootheid wordt vaak de kleine letter \(c\) gebruikt. Als kJkg\(^{-1}\)K\(^{-1}\) de eenheid voor \(c\) is, dan geldt \(C=mc\), met \(m\) de massa van het lichaam.

Meting van de soortelijke warmte

Een eenvoudig apparaat voor meting van de soortelijke warmte van een stof is de watercalorimeter. Dat is een thermisch geïsoleerd vat, gevuld met water. De meting gaat als volgt. Een lichaam van de te onderzoeken stof met temperatuur \(T_N\) wordt ondergedompeld in het water. Aanvankelijk hebben het water en de calorimeter een temperatuur \(T_W\) die iets boven kamertemperatuur ligt. Na onderdompeling bereiken de koperen cilinder, het water en de calorimeter uiteindelijk een gemeenschappelijke eindtemperatuur \(T_f\), met \(T_N<T_f<T_W\). Als er geen warmte uitwisseling is met de omgeving, geldt de volgende warmtebalans (``opgenomen warmte is afgestane warmte’’):

()\[ \left|\Delta Q_{\mathrm{Cu}}\right|=\left|\Delta Q_{w, c}\right| \]

Hierin is \(\Delta Q_\mathrm{Cu}\) de hoeveelheid warmte die door de koperen cilinder is opgenomen bij het opwarmen van \(T_N\) tot \(T_f\) en \(\Delta Q_{w,c}\) de hoeveelheid warmte die door de watercalorimeter is afgestaan bij het afkoelen van \(T_W\) tot \(T_f\). We nemen absolute waardes om ons niet te hoeven bekommeren om de tekenconventies van opgenomen en afgestane warmte. Uit formule () volgt dat deze hoeveelheden warmte te schrijven zijn als een integraal over de warmtecapaciteit, zodat vergelijking () overgaat in:

()\[ \int_{T_N}^{T_f} C_{\mathrm{Cu}}(T) dT=\int_{T_f}^{T_W}\left[C_{\mathrm{H}_{2} \mathrm{O}}(T)+C_{\mathrm{vat}}(T)\right] dT \]

\(C_\mathrm{Cu}\), \(C_\mathrm{H_2 O}\) en \(C_\mathrm{vat}\) zijn respectievelijk de warmtecapaciteit van de koperen cilinder, het water in de calorimeter en het calorimetervat. Uitwerken van vergelijking () levert:

()\[ \int_{T_N}^{T_f} m_{\mathrm{Cu}} c_{\mathrm{Cu}}(T) dT=\int_{T_f}^{T_W}\left[m_{\mathrm{H}_{2} \mathrm{O}} c_{\mathrm{H}_{2} \mathrm{O}}(T)+C_{\mathrm{vat}}(T)\right] dT \]

waarin \(m_{\mathrm{Cu}}\) de massa van de koperen cilinder is en \(m_\mathrm{H_{2}O}\) de massa van het water, \(c_{\mathrm{Cu}} (T)\) is de soortelijke warmte van koper en \(c_\mathrm{H_2 O}(T)\) is de soortelijke warmte van water. Als we nu het experiment zo inrichten dat de temperatuurverandering van \(T_W\) naar \(T_f\) klein is, mogen we \(c_\mathrm{H_2 O} (T)\) en \(C_\mathrm{vat} (T)\) constant veronderstellen, zodat formule () overgaat in:

()\[ m_{\mathrm{Cu}} \int_{T_N}^{T_f} c_{\mathrm{Cu}}(T) d T=\left(m_{\mathrm{H}_{2} \mathrm{O}} c_{\mathrm{H}_{2} \mathrm{O}}+C_{\mathrm{vat}}\right) \int_{T_f}^{T_W} d T \]

Met de definitie van de gemiddelde soortelijke warmte over het interval van \(T_N\) tot \(T_f\):

()\[ \overline{c_{\mathrm{Cu}}}=\frac{\int_{T_N}^{T_f} c_{\mathrm{Cu}}(T) d T}{T_f-T_N} \]

gaat formule () over in:

()\[ \overline{c_{\mathrm{Cu}}}=\frac{m_{\mathrm{H}_{2} \mathrm{O}} c_{\mathrm{H}_{2} \mathrm{O}}+ C_{\mathrm{vat}}}{m_{\mathrm{Cu}}}\left(\frac{T_W-T_f}{T_f-T_N}\right) \]

Door nu de verhouding \(\frac{T_f-T_N}{T_W-T_f}\) te bepalen als functie van \(m_{H_2 O}\), kan de gemiddelde soortelijke warmte van koper over het interval \(T_N\) tot \(T_f\) bepaald worden. Hiervoor hoeven we \(C_{vat}\) niet te kennen.

In de praktijk valt aan de voorwaarde dat er geen warmte uitwisseling is met de omgeving moeilijk te voldoen. Om de invloed van deze uitwisseling klein te houden, kunnen we het experiment zo inrichten dat de verandering van watertemperatuur \(T_W\) naar eindtemperatuur \(T_f\) rond kamertemperatuur \(T_{kamer}\) ligt. We zorgen ervoor dat kamertemperatuur dus steeds halverwege tussen de begin- en de eindtemperatuur van het water in de calorimeter ligt: \(T_{kamer}\approx\frac{T_W+T_f}{2}\). Een eventueel warmtelek naar de omgeving keert dan tijdens het proces van teken om, zodat het positieve en negatieve warmtelek elkaar min of meer compenseren. Voor dat doel is de calorimeter met een stookelement uitgerust. In deze proef is het lichaam een cilinder van koper en is \(T_N\) gelijk de kooktemperatuur van vloeibare stikstof (\(T_N\)=77 K).

Vergelijking met de theoretische waarde

Experimenten worden doorgaans gedaan om een bepaalde theorie te testen. In dit geval willen we de gemeten soortelijke warmte vergelijken met de waarde die de theorie van Einstein voor de soortelijke warmte van een vaste stof voorspelt. Volgens Einstein wordt de soortelijke warmte gegeven door:

()\[ c_{E}(T)=\frac{3 R}{M} \frac{\left(\theta_{E} / T\right)^{2} e^{\theta_{E} / T}}{\left(e^{\theta_{E} / T}-1\right)^{2}} \]

Hierin is \(\theta_E\) de Einsteintemperatuur, een karakteristieke temperatuur die een maat is voor de trillingsenergie van de atomen in het kristalrooster van de stof. De waarde van \(\theta_E\) hangt af van de soort stof, zodat het gaat om de Einsteintemperatuur van koper (\(\theta_\textrm{E,Cu}\)=240 K). \(R\) is de gasconstante ( \(R\)=8.3144 JK\(^{-1}\)mol\(^{-1}\) ) en \(M\) is de molmassa van koper (\(M_\textrm{Cu}\)=63.55 kg kmol\(^{-1}\)). De functie gegeven door formule () is voor koper afgebeeld in Figuur {number}.

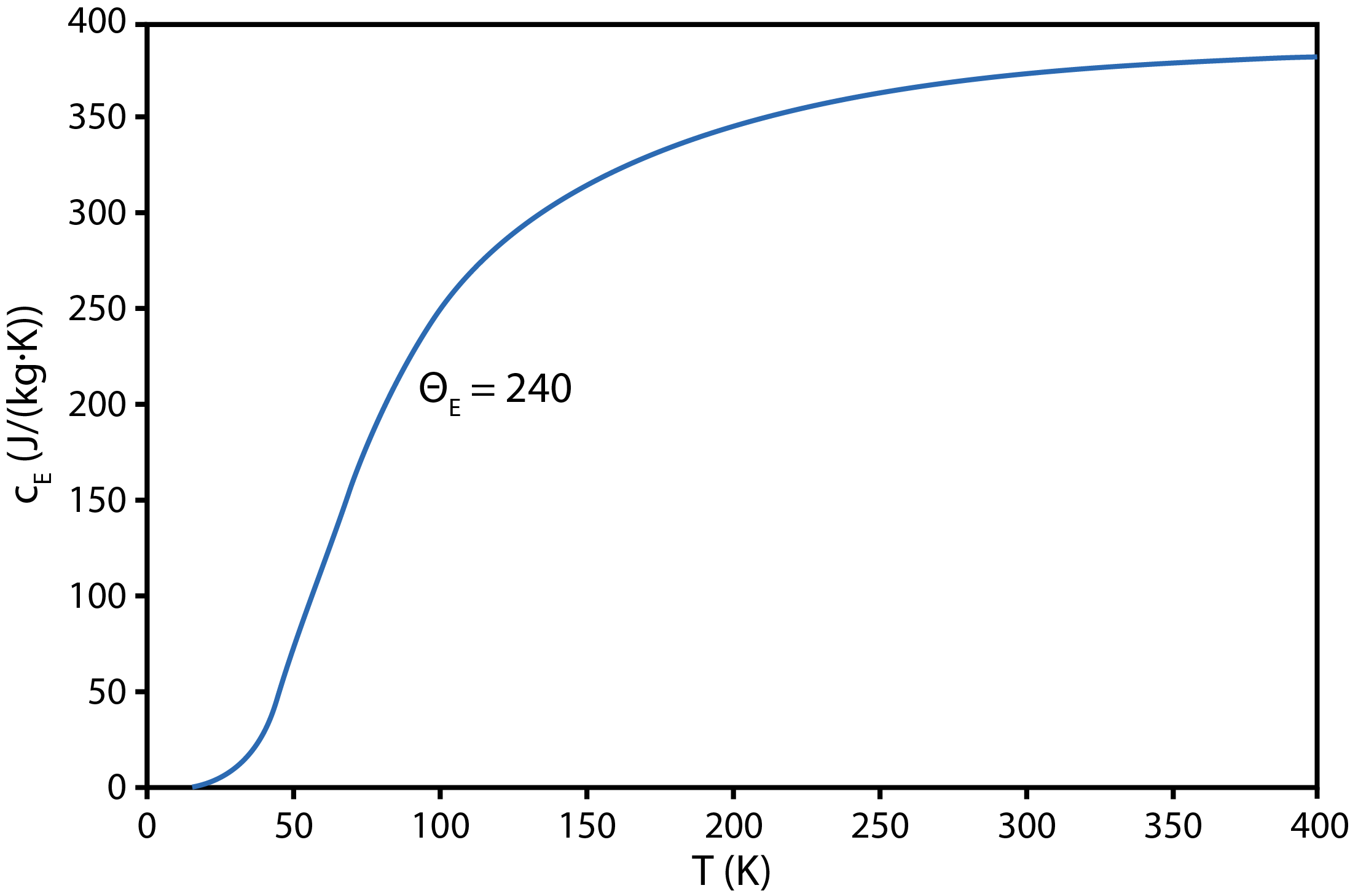
Soortelijke warmte als functie van de temperatuur volgens het Einsteinmodel, voor \(\theta_{E,Cu}\)=240 K

Als we formule () voor \(c_E (T)\) invullen in formule (), geeft dat een nogal ingewikkelde integraal (hoewel je over niet al te lange tijd zelf de primitieve zult kunnen uitrekenen). Daarom wordt hier het eindresultaat gegeven voor de gemiddelde soortelijke warmte volgens Einstein:

()\[ \overline{c_{\mathrm{Cu}}}\left(T_{1\mathrm{CE}}\right) =\frac{3 R \theta_{E}}{M\left(T_f-T_N\right)}\left\{\frac{1}{e^{\theta_{E} / T_f}-1}-\frac{1}{e^{\theta_{E} / T_N}-1}\right\} \]

Hiermee kun je de theoretische waarde uitrekenen.

Opdrachten

De probleemstelling staat geschreven bij het doel. Voor de probleemanalyse en het opstellen van het meetplan is een aparte middag ingeroosterd. In deze fase is het van belang aan de volgende punten aandacht te besteden.

• Bestudeer de verstrekte apparatuur. Volgens de fabrikant van de Thurlby 1905 Intelligent multimeter is de gevoeligheid van dit apparaat 1 μV. Klopt dat?

• Lees in de volgende sectie het stuk over de thermokoppel. We gebruiken de thermokoppel omdat deze verwerkt kan worden in het koperen blokje en dus nauwkeuriger de temperatuur van het koperen blokje meet.

• Bedenk de procedure die je gaat volgen voor het kalibreren van het thermokoppel en noteer die.

• Hoe zorg je voor de temperatuur van smeltend ijs voor de referentielas?

• Maak een kwalitatieve schets in één figuur het verwachte globale temperatuurverloop in de tijd van de koperen cilinder en van het water, d.w.z. van \(T_N\) en \(T_W\).

• Leid formule () af uit formules () en ()

• Leg uit hoe je door \(\frac{T_f-T_N}{T_W-T_f}\) als functie van \(m_{H_2 O}\) te meten de gemiddelde soortelijke warmte van koper in het interval van \(T_N\) tot \(T_f\) kan bepalen. Welke aanname maak je daarbij?

• Leid de formule af voor de absolute onzekerheid in \(\frac{T_f-T_N}{T_W-T_f}\) .

• Schat met behulp van de curve in Figuur 2 de gemiddelde soortelijke warmte van koper op het temperatuurinterval dat begint bij het kookpunt van vloeibare stikstof en eindigt bij kamertemperatuur. Gebruik formule () om deze schatting te controleren.

• Stel een formule op waarmee je de temperatuurverandering van het water in de calorimeter kan schatten. Verwaarloos daarbij de warmtecapaciteit van het calorimetervat. Kies realistische waardes van de grootheden en bereken de temperatuurverandering.

• De aanname in formule () dat (\(\overline{c_\textrm{Cu}}\) ) een contante is, d.w.z. niet afhangt van eindtemperatuur \(T_f\) is feitelijk onjuist (waarom?). In dit verband: vergelijk de spreiding in (\(\overline{c_\textrm{Cu}}\) ) volgens formule () voor verschillende \(T_f\) met de onzekerheid in de gemeten gemiddelde soortelijke warmte en bediscussieer deze vraagstelling in het verslag.

• Stel een meetplan op. Bespreek dit met de assistent van de proef. Doe eventueel een proefmeting. Na goedkeuring door de assistent voer je het meetplan uit op de daarvoor bestemde middag. Gebruik bij de dataverwerking Python. Vraag, indien nodig, de assistent om uitleg.

Thermokoppel

Een thermokoppel is een temperatuursensor bestaande uit twee metalen of metaallegeringen. Als er een temperatuurverschil zit tussen beide contactpunten, zie Figuur {number}, zal er een potentiaalverschil ontstaan.

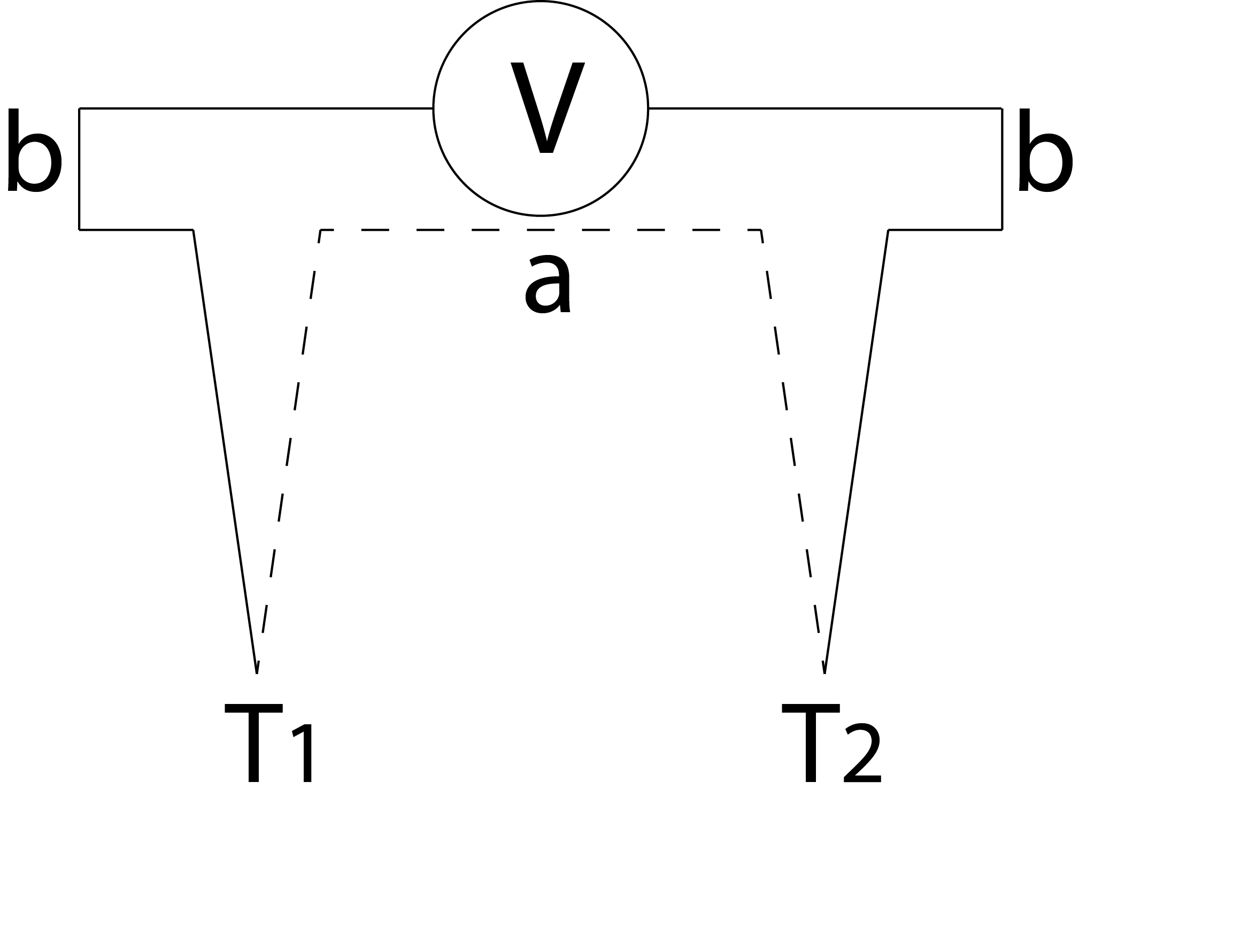
Principe van temperatuurmeting met een thermokoppel

In Figuur {number} zijn a en b verschillende metalen, bijvoorbeeld koper en constantaan, die op twee punten verbonden (“gelast”) zijn. Bevinden beide lassen zich op een verschillende temperatuur, dan ontstaat tussen de lassen een spanningsverschil , dat een maat is voor het temperatuurverschil. Dit spanningsverschil heet thermospanning. Meestal wordt één van de lassen op een constante referentietemperatuur gehouden (bijvoorbeeld 0 \(^o\)C, de temperatuur van smeltend ijs) en is de tweede las de meetlas. Voordat het thermokoppel gebruikt kan worden, moet het eerst gekalibreerd worden. Voor een beperkte temperatuurgebied rond kamertemperatuur kunnen we volstaan met een lineaire relatie tussen de (Celsius)temperatuur \(t\) van de meetlas en de thermospanning:

\[ t=AV+B \]

De coëfficiënten \(A\) en \(B\) kunnen bepaald worden met een kleinste kwadraten aanpassing.

Literatuur

Voor nadere gegevens en gedetailleerdere theorie kun je raadplegen (in de practicumzaal aanwezig):

1. James, A.M. and M.P. Lord, Macmillan’s Chemical and Physical Data, Macmillan Press, 1992.

2. Tabor, G., Gases, Liquids and Solids, Cambridge University Press, 1991.