11. De magneetzweeftrein#

11.1. Doelen & structuur#

Tip

In elke practicumhandleiding vind je twee soorten doelen. De practicumdoelen vertellen wat je in het practicum gaat doen. De leerdoelen geven aan wat we willen dat je hebt geleerd na het doen van het practicum.

11.1.1. Practicumdoel#

In dit practicum bepaal je de wiskundige relatie tussen de kracht en de afstand tussen twee magneten.

11.1.2. Leerdoel#

Na het uitvoeren van dit practicum:

  • Weet je de weg te vinden bij het natuurkundig practicum en ben je bekend met de procedure van het practicum.

  • Ken je de basisbegrippen meetbereik, interval, herhaalbaarheid, reproduceerbaarheid en kun je deze toepassen in een onderzoek.

  • Kun je meetfouten en meetonzekerheden door rekenen.

  • Kun je data analyseren en presenteren m.b.v. Python.

  • Ken je de basisprincipes en onderdelen van een verslag in het algemeen en specifiek resultaten, discussie en conclusie.

11.1.3. Structuur#

Inleiding Experimenteren 1 (IE-1) bestaat uit verschillende delen:

  • Voorbereiding & Uitvoering

  • Analyseren van de data

  • Verslagmiddag 1

  • Geven en ontvangen van feedback

  • Verslagmiddag 2

Het verslag maak je met de partner waarmee je samenwerkt.

11.2. Inleiding#

Magneetzweeftreinen blijven vlak boven de grond zweven doordat ze gebruik maken van magneten die elkaar afstoten en aantrekken. In het ontwerpen van de magneetzweeftrein is het modelleren van het gedrag van de trein bij hoge snelheden van groot belang. Zonder een goed computermodel zal het niet mogelijk zijn om een goed werkend prototype te maken.

Een van de factoren die van invloed is op het gedrag van de trein is de afstand tussen de grond en de trein en de demping wanneer er over een niet volledig horizontaal traject wordt gereden. Om dat te kunnen modelleren is het van belang dat de precieze relatie tussen de afstand tussen de magneten en de grootte van de afstotende kracht bekend is. Alhoewel de theorie een goede indruk geeft van deze relatie, zal deze relatie voor niet geïdealiseerde situaties experimenteel bevestigd moeten worden. Het is belangrijk om inzicht te krijgen in hoeverre de geïdealiseerde theorie in staat is de praktijk te benaderen (of vice versa). De onderzoeksvraag wordt daarmee:

Hoe hangt de kracht tussen twee tegenover elkaar geplaatste schijfmagneten af van de afstand tussen de magneten?

Note

De hoofdonderzoeker die het onderzoek zou uitvoeren is in het buitenland en kan onmogelijk het onderzoek afronden. Jij en je partner zijn aangesteld als de vervanger van de hoofdonderzoeker en moeten een overtuigend antwoord op deze onderzoeksvraag geven. Gelukkig ligt er een theoretische afleiding voor een natuurkundig model en zijn er door de hoofdonderzoeker een introductie en methode geschreven. Deze staan hieronder uitgewerkt. De methode is goed genoeg beschreven om de daadwerkelijke metingen uit te voeren. Helaas zijn wel alle meetonzekerheden en de daarbij behorende berekeningen niet uitgevoerd. Ook die berekeningen en afleidingen moeten door jullie gemaakt worden.

Uit het rapport van de onderzoeker

11.3. Theoretische achtergrond#

11.3.1. Schijfmagneten#

In dit experiment wordt gebruik gemaakt van twee schijfmagneetjes. Een schijfmagneetje is een kleine magneet in de vorm een platte cilinder, zie Figuur 11.1. De permanente schijfmagneetjes van deze proef zijn gemaakt van de ferromagnetische verbinding Nd\(_2\)Fe\(_{14}\)B. Het symbool Nd staat voor het zeldzame aardmetaal neodynium. Fe staat voor het element ijzer, terwijl het symbool B het element boor aanduidt. Nd\(_2\)Fe\(_{14}\)B magneten zijn de sterkste commercieel verkrijgbare magneten en worden toegepast in o.a. motoren, luidsprekers en magnetische lageringen. Zelfs bij de kleine afmetingen als gebruikt in deze proef zijn Nd\(_2\)Fe\(_{14}\)B magneten zeer krachtig.

../_images/magneten.png

Fig. 11.1 Krachten tussen schijfmagneetjes in geval van aantrekking. \(F_{21}\) is de kracht die magneet 2 uitoefent op magneet 1 en \(F_{12}\) is de kracht die magneet 1 uitoefent op magneet 2. De twee afstanden tussen de magneetjes zijn aangeduid.#

11.3.2. Magnetische dipolen#

Eigenschappen van het magnetisch veld van een schijfmagneet kunnen grotendeels afgeleid worden uit de benadering dat een schijfmagneet opgevat mag worden als een klassieke magnetische dipool. Een klassieke magnetische dipool is een kleine draadlus waardoorheen een elektrische stroom loopt. Figuur 11.2geeft een voorstelling van zo’n dipool met het bijbehorend patroon van magnetische veldlijnen. De dipool wordt gekarakteriseerd door het magnetisch dipoolmoment \((\vec{m}=I\vec{A})\), een vector (met grootte en richting). Hierin is:

  • \(I\) de grootte van de stroom door de lus in A

  • \(A\) het oppervlak van de lus in m\(^2\)

  • \(m\) het magnetische dipoolmoment in Am\(^2\)

Het oppervlak is hier een vector waarvan de richting bepaald wordt door de richting van de stroom en gevonden kan worden met behulp van de rechterhandregel. Een puntdipool ontstaat in de limiet waarbij het oppervlak van de lus naar nul gaat en de stroom naar oneindig, zodanig dat het product \(\vec{m}=I\vec{A}\), constant blijft.

../_images/magneetvelden.png

Fig. 11.2 Klassieke magnetische dipool (a), gevormd door een stroomvoerende draadlus, met het bijbehorend patroon van magnetische veldlijnen. Ferromagetische dipool (b), opgebouwd uit een N-pool en een Z-pool, eveneens met veldlijnenpatroon. Naar [1], na aanpassing.#

Kleine ferromagneten zoals de magneetschijven in dit experiment zijn ook magnetische dipolen, die je opgebouwd kan denken uit een noordpool (N-pool) en een even sterke zuidpool (Z-pool) met een kleine tussenafstand tussen de polen. In Figuur 11.2 b is een magnetische dipool met het veldlijnenpatroon afgebeeld. Het magnetisch veld van de klassieke en ferromagnetische dipool hebben hetzelfde ruimtelijke patroon. Als een ferromagneet maar klein genoeg is, kan deze ook gezien worden als een puntdipool. Omgekeerd, gezien van grote afstand, gedraagt iedere magnetische dipool (bijvoorbeeld de aarde) zich als een magnetische puntdipool.

11.3.3. De kracht tussen magnetische dipolen#

Twee magneten oefenen niet alleen een aantrekkende of afstotende kracht op elkaar uit, maar ook een moment: ze oriënteren zich in elkaars veld. Het richten van een kompasnaald in het aardmagnetisch veld is een bekend voorbeeld van dit effect.

In dit experiment concentreren we ons alleen op de kracht tussen magneten. Om daarvoor een formule te vinden, starten we vanaf de wisselwerkingsenergie \(U\) van twee magnetische puntdipolen \((\vec{m_1})\) en \((\vec{m_2})\) op onderlinge afstand \((\vec{r})\). Dat is de potentiële energie van één van de dipolen in het magnetisch veld van de andere. Zonder afleiding presenteren we hier de formule voor \(U\):

(11.1)#\[ U=\frac{\mu}{4\pi}\left(\frac{\vec{m_1}\cdot\vec{m_2}}{r^3}-\frac{3(\vec{m_1}\cdot\vec{r})(\vec{m_2}\cdot\vec{r})}{r^5}\right ) \]

Hierin is \(\mu\) is de permeabiliteit van het medium en \((\vec{r})\) de vector die dipool 1 verbindt met dipool 2. Voor lucht als medium mag \(\mu_0\) genomen worden, de permeabiliteit van het vacuüm. De producten in formule (11.1) met een punt (\(\cdot\)) zijn zogenoemde inwendige producten (pro memorie: \(\vec{a}\cdot\vec{b}=|\vec{a}| |\vec{b}|\cos(\theta)\) met \(\theta\) de hoek tussen de vectoren \((\vec{a})\) en \((\vec{b})\) ). Als geldt \((\vec{m_1}=\vec{m_2}=m)\) en als de dipoolmomenten antiparallel of parallel langs de verbindingsvector \((\vec{r})\) liggen, reduceert formule (11.1) voor lucht als medium tot:

(11.2)#\[ U=\pm \frac{\mu_o}{2\pi}\frac{m^2}{z^3} \]

De energie is positief als de dipolen antiparallel zijn (afstoting) en negatief als deze parallel zijn (aantrekking). In formule (11.2) is de afstand \(r\) vervangen door de verticaal veronderstelde afstand \(z\) (als in het experiment). Aangezien de kracht de plaats afgeleide is van de potentiële energie, geldt er voor de magnetische kracht tussen de dipolen (we negeren hier de richting van de kracht en definiëren impliciet de constante \(\alpha\)):

(11.3)#\[ F_m(z) = \frac{dU}{dz} = \frac{3\mu_0m^2}{2\pi}\frac{1}{z^4}=\frac{\alpha}{z^4} \]

Vaak wordt ter karakterisering van een permanente magneet het remanente veld \(B_r\) gebruikt [2]. Dat is het magnetisch veld van de magneet dat permanent overblijft of achterblijft na magnetisatie. Het remanente veld wordt geven door:

(11.4)#\[ B_r = \mu_0 \frac{m}{V} \]

In formule (11.4) is \(V\) het volume van de magneet, zodat het remanente veld gezien kan worden als een dipool-dichtheid.

De hier gepresenteerde theorie is van toepassing op puntdipolen. De schijfmagneetjes van deze proef zijn echter geen punten, maar hebben een zekere ruimtelijke uitgebreidheid. Daarom kan in het experiment mogelijk een afwijking gevonden worden van de afstandsafhankelijkheid als beschreven door formule (11.3).

11.4. Introductie#

Voor het ontwerpen van nieuwe, snellere en veiligere zweeftreinen is het essentieel om accurate computermodellen te gebruiken die het rijgedrag van de zweeftrein kunnen simuleren. Voor een accuraat computermodel is een model van de relatie tussen de afstand tussen de twee magneten en de onderlinge kracht essentieel [3]. In dit onderzoek wordt een model dat gebaseerd is op de superpositie van magnetische puntdipolen getest.

Het model, afgeleid en beschreven in [4], gaat ervan uit dat de totale potentiele energie van de magneten gelijk is aan de som van potentiele energie van magnetische puntdipolen. Met het gegeven dat de kracht gelijk is aan de afgeleide van de potentiele energie naar de afstand, geldt voor de kracht tussen twee magneten:

(11.5)#\[ F_{m}(z)=\frac{3 \mu_{0} m^{2}}{2 \pi} \frac{1}{z^{4}}=\alpha \frac{1}{z^{4}} \]

Hierin is \(\mu_0\) de magnetische permeabiliteit, \(m\) het magnetische dipoolmoment en \(z\) de hart-tot-hart afstand van de twee magneten. Dit model wordt gevalideerd aan de hand van een experimentele opzet waarbij de afstotende en aantrekkende kracht tussen twee magneten en hun onderlinge afstand wordt bepaald. Uit het experiment wordt het remanente veld bepaald:

(11.6)#\[ B_{r}=\mu_{0} \frac{m}{V} \]

Het model is gevalideerd wanneer de experimentele waarden het verwachtte vierde machtsverband gedrag vertonen en het remanente veld volgend uit de empirische data overeenkomt met de specificaties van de magneten. Daartoe richten we ons op de volgende twee onderzoeksvragen:

  • Hoe hangt de afstotende/aantrekkende kracht tussen twee magneten af van hun onderlinge afstand?

  • Is het theoretische model van een superpositie van dipolen voldoende om die relatie te beschrijven?

Dit onderzoek is uitgevoerd als onderdeel van het vak Natuurkundig Practicum aan de TU Delft.

11.5. Experimentele methode#

11.5.1. Experiment en instrumentatie#

Voor het valideren van het voorgestelde model wordt gebruik gemaakt van een opstelling waarbij twee magneten boven elkaar hangen en de onderlinge kracht bepaald wordt, zie Figuur 11.3. De hart-tot-hart afstand tussen de twee magneten, zie Figuur 11.4, wordt gegeven door:

(11.7)#\[ z=\frac{1}{2} d_{m}+h_{1}+h_{1,2}+h_{2}+\frac{1}{2} d_{m} \]

Voor bepaling van \(h_1\) en \(h_2\) wordt een schuifmaat gebruikt met een meetonzekerheid van … mm, \(h_{1,2}\) wordt bepaald m.b.v. een liniaal met een meetonzekerheid van … mm. Volgens de specificatie van de magneet is de meetonzekerheid in de dikte van de magneet … mm [2]. Dit levert een totaal meetonzekerheid van \(\mu_r\)= … mm. Zie de Appendix voor de bijbehorende afleiding.

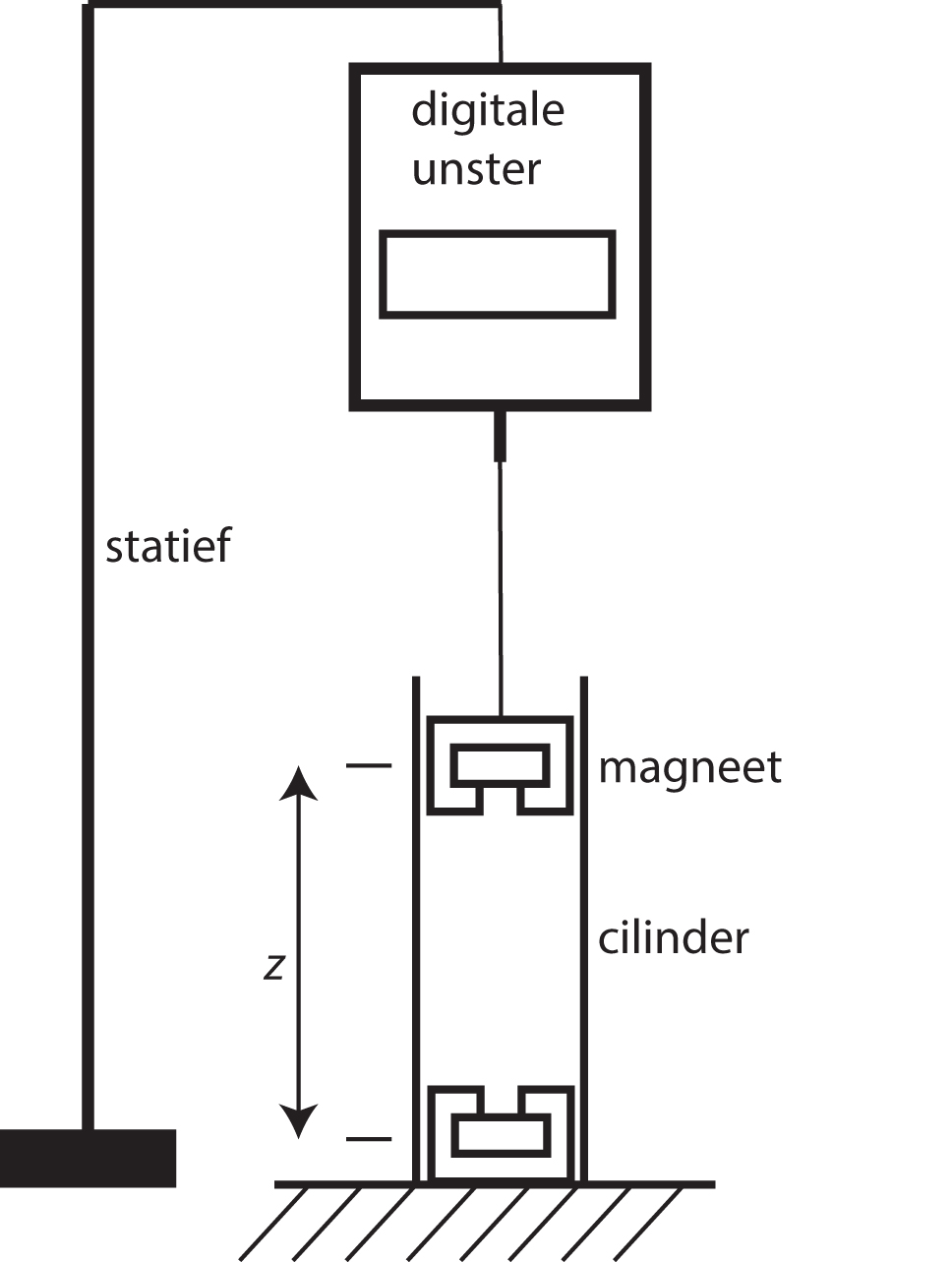
../_images/opstelling.jpg

Fig. 11.3 De opstelling waarbij de bovenste magneet gepositioneerd wordt t.o.v. de gefixeerde magneet. De onderlinge kracht wordt bepaald m.b.v. een digitale unster.#

Met behulp van een digitale unster (Christen Orange OR-42) met een afleesnauwkeurigheid van … g wordt de onderlinge uitgeoefende kracht bepaald:

(11.8)#\[ F_{1,2}=\Delta m \cdot g \]

hierin is \(g\) de zwaartekrachtsversnelling in Nederland met een waarde van 9.812 ± 0.001 m/s² en \(\Delta\)m het verschil in massa in kg gegeven door:

\[ \Delta m=m_{\infty}-m_{r} \]

Hier is \(m_{\infty}\) de massa op ‘oneindige’ afstand van de vaste magneet en \(m_r\) de gemeten massa op afstand \(r\) van de vaste magneet. Aangezien de meetonzekerheid in \(g\) velen malen kleiner is dan de meetonzekerheid in \(m\), geldt \(u(F)\) = 1\(\cdot10^{-2}\) N, zie de appendix voor de afleiding.

11.5.2. Procedure#

In de eerste meetserie wordt gebruik gemaakt van twee aantrekkende magneten. De bovenste magneet wordt langzaam naar de onderste magneet bewogen. Het punt waarbij de eerste uitwijking van de unster (\(\Delta m \ne 0\)) en de grootst mogelijke kracht tussen de magneten wordt bepaald. Vervolgens worden de daadwerkelijke metingen uitgevoerd met een krachtsinterval van grofweg \(\frac{F_{max}-F_{min}}{10}\). Deze keuze voor interval zorgt er voor dat met name op korte afstanden, overeenkomstig met de afstand tussen de magneten van treinen, veel metingen gedaan worden. Bovenstaande procedure wordt herhaald voor een verzwaarde afstotende magneet.

../_images/ie1_opst_onz.png

Fig. 11.4 De close up van de twee magneten (grijs) in hun plastic omhulsel laat de verschillende te bepalen grootheden zien, waarbij de hart-tot-hart afstand gegeven wordt door formule (11.7)#

Einde rapport van de onderzoeker

11.6. Opdrachten practicummiddag#

Voer de volgende opdrachten uit:

  • Meet alle afstanden uit Vergelijking (11.7) behalve \(h_{1,2}\).

  • Doe de afleiding voor de onzekerheid in de afstand en de kracht. Deze zouden beschreven staan in de Appendix, maar de Appendix is niet terug te vinden in de documenten van de hoofdonderzoeker.

  • Volg de beschreven meetprocedure. Voer de definitieve metingen uit voor de relatie tussen kracht en afstand. Noteer de uitkomsten in de excel (zie Brightspace). Noteer de meetonzekerheden in het Jupyter Notebook (labjournaal).

  • Verwerk alle metingen in de Jupyter Notebook (te vinden op Brightspace).

  • Maak de eerste plot.

  • Laat je plot controleren door de TA.

11.7. Opdrachten data-analyse#

Je hebt je data verzameld en een eerste plot gemaakt. Nu ga je de data analyseren door :

  • Een errorbarplot te maken met curve fit.

  • Te onderzoeken of er eventueel sprake is van een systematische fout en daarvoor compenseren.

  • Het vierde machtsverband onderzoeken met behulp van een linearisatie.

  • Het remanente veld berekenen en vergelijken met het remanente veld gemeld in de specificaties.

Om je te helpen bij deze analyse, staan de stappen ook vermeld in het notebook.

11.7.1. Referenties#

1

I. S. Grant and W. R. Phillips. Electromagnetism, The Manchester physics series, 2nd ed. Wiley, Chichester [England] ; New York, 2008.

2(1,2)

Supermagnete. Data_sheet_s-10-05-n.pdf. Technical Report, 2011. URL: https://www.supermagnete.nl/data_sheet_S-10-05-N.pdf.

3

Y. Sanagawa, H. Ueda, M. Tsuda, A. Ishiyama, S. Kohayashi, and S. Haseyama. Characteristics of lift and restoring force in hts bulk-application to two-dimensional maglev transporter. IEEE transactions on applied superconductivity, 2001.

4

C.F.J Pols. IE 1: De magneetzweeftrein. Technische Universiteit Delft, 2019.