Spectroscopie#
Doel#
In deze proef bestuderen we eerst het licht dat wordt uitgezonden door een kwiklamp (Hg) of een natriumlamp (Na). Het spectrum van deze bronnen bestaat uit een aantal heldere spectraallijnen. Het doel van deze proef is de golflengte van deze lijnen zo nauwkeurig mogelijk te bepalen. We maken daarbij gebruik van een optisch tralie. Een vraag die daarbij opkomt is: hoe klein is het relatieve golflengteverschil van twee spectraallijnen die met onze opstelling als net gescheiden worden weergegeven?
Voor de uitvoering van dit practicum als open proef is het volgen van de onderstaande handleiding een must, maar onvoldoende omdat het volgen is van een recept. Voor een eigen onderzoek kun je denken aan andere lampen, het verwisselen van lenzen, een andere slitgrote, gebruik van een cd ipv grating etc.
Voorbereiding#
Als je op het practicum komt, word je geacht dit hoofdstuk van de handleiding goed te hebben bestudeerd en de antwoorden van de elf vragen die hier in voorkomen in je labjournaal te hebben opgeschreven. Komen er bij de bestudering bij jou nog andere vragen op? Noteer deze vragen dan ook in je labjournaal en stel ze aan het begin van het practicum.
Installeer de Thorlabs software voor de camera, deze vind je hier.
Theoretische achtergrond#
Wat is een tralie?#
Een tralie is een plaat waarop een zeer groot aantal evenwijdige lijnen aanwezig zijn, die onderling op gelijke afstand van elkaar lopen. Een schematische weergave is te zien in Figuur {number}.
Typische afmetingen zijn 5x5 cm en een typische waarde voor het aantal lijnen per mm ligt in de range 100 - 1000. Een tralie kan doorlatend of spiegelend zijn. Men spreekt dan van, respectievelijk, een transmissie- of een reflectietralie.

Schematische weergave van een tralie. Typische afmetingen zijn 5x5 cm. Het aantal lijnen per mm ligt in de range 100 – 1000.#
Wat doet een tralie?#
Een tralie is een optisch instrument dat licht afbuigt. Hoe groter de golflengte, hoe groter de afbuiging. In Figuur {number} is weergegeven wat er gebeurt als ‘wit’ licht met een continu kleurenspectrum tussen blauw en rood op een transmissietralie valt. Een deel van het licht gaat gewoon rechtdoor en de kleur van dat licht is nog steeds wit. Dit is het 0-de orde buigingspatroon. Onder en boven daarvan zien we spectaculaire banden waarvan de kleur verloopt van blauw naar rood. Dit zijn de 1-ste orde buigingspatronen. Deze patronen kunnen zich bij grotere buigingshoeken nog meerdere keren herhalen (2-de orde, 3-de orde, ..).
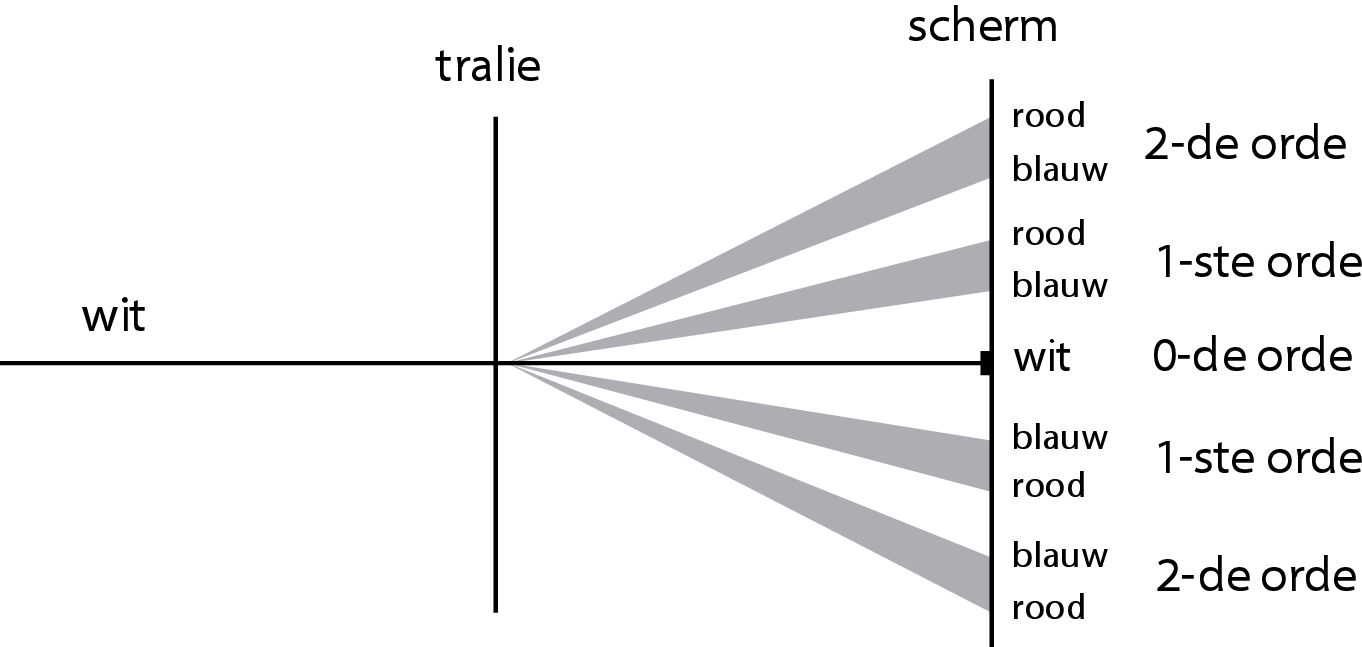
Een transmissietralie in werking. Wit licht met een continu kleurenspectrum van blauw naar rood wordt gesplitst in verschillende kleuren en ordes.#
Lichtstralen en golffronten#
In deze proef komt vooral het golfkarakter van licht aan bod. Hierbij draait het om begrippen als interferentie en buiging (diffractie). Om buigingsverschijnselen te verklaren, wordt vaak een beroep gedaan op het principe van Huygens (zie onder). Dit principe zegt iets over de uitbreiding van golffronten. Wat is een golffront?
Een golffront is een verzameling punten waarvan de “trilling” dezelfde fase heeft. Als we naar watergolven kijken, zien we in feite de golffronten. Gooien we een steentje in het water dan zien we golffronten die zich cirkelvormig uitbreiden. Kijken we naar golven die het strand opspoelen dan zien we een serie evenwijdige golffronten. Deze karakteristieke golffronten zijn schematisch in Figuur {number} weergeven.
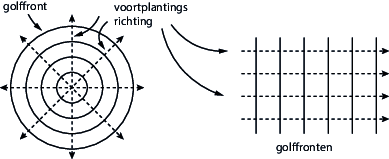
Twee karakteristieke golfpatronen. Links: de uitbreiding van cirkel (bol) -vormige golffronten. Rechts: naar rechts lopende rechte (vlakke) golffronten (= evenwijdige lichtbundel).#
De relatie met lichtstralen is dat een lichtstraal de voortplantingsrichting van het licht in een bepaald punt weergeeft. Plant een golf zich in een isotroop medium voort dan staat de richting hiervan loodrecht op het golffront, zie Figuur {number}.
Principe van Huygens (Wolfson, hfdst. 32.5)
Alle punten op een golffront werken als puntbronnen voor bolvormige “golfjes” die zich uitbreiden met de lichtsnelheid in het medium. Een korte tijd \(\Delta t\) later wordt het nieuwe golffront gevormd door dat oppervlak dat raakt aan alle “golfjes” die zich in de voortplantingsrichting uitbreiden.*
In Figuur {number} is weergegeven hoe dit werkt. Links zien we hoe een bolvormig golffront op tijdstip \(t\) zich ontwikkelt naar een nieuw bolvormig golffront op \(t+\Delta t\). Voor vier punten op het golffront op \(t = t\) is aangegeven hoe de golfjes zich in een tijdsinterval \(\Delta t\) uitbreiden. Het nieuwe golffront op \(t + \Delta t\) is raak-“lijn” aan deze golfjes.
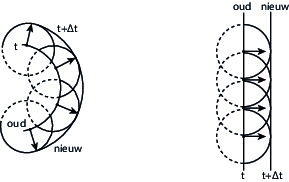
Voortplanting van een golffront volgens het principe van Huygens. Links een bolvormig golffront en rechts een vlak golffront.#
In Figuur {number} rechts wordt op dezelfde manier de voortplanting van een vlak golffront geconstrueerd. Zoals gezegd, het principe van Huygens is hèt hulpmiddel om de buiging van licht te verklaren. Als eerste toepassing bekijken we wat er gebeurt als een vlakke golf op een scherm met een gaatje valt. De diameter van het gaatje is vergelijkbaar met of kleiner dan de golflengte van het licht. Zie Figuur {number}.
Een vlakke golf valt vanaf de linkerkant op het scherm. Het licht dat in de opening terecht komt gaat volgens Huygens als een puntbron bolvormige golven uitzenden. Als het gaatje van de orde van de golflengte is, wordt een groot deel van het licht afgebogen. Dit gedrag heb je vast wel eens gezien in demonstratie experimenten met een waterbak. Als dat niet zo is, kijk op YouTube. Zoek op: ripple tank diffraction. In Fig. 32.22 (c) van Wolfson kun je ook zien hoe de intensiteit van het licht dan verloopt.
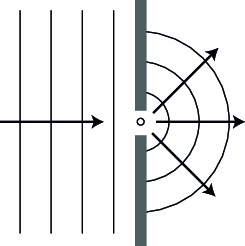
Een vlakke lichtgolf valt op een scherm met een gaatje met een diameter vergelijkbaar met de golflengte. Volgens het principe van Huygens werkt het gaatje als een puntbron die bolvormige golven uitzendt.#
Interferentie#
De volgende vraag is: wat er gebeurt als er twee gaatjes in het scherm zitten? Zie Figuur {number}.
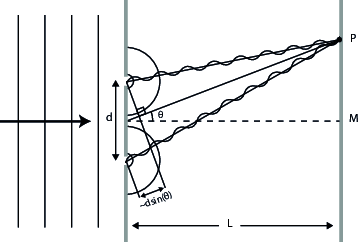
Een vlakke lichtgolf valt op een scherm met twee gaatjes. Deze gaatjes werken als puntbronnen die in fase bolvormige golven uitzenden. In de hier geschetste situatie interfereren beide golven in punt P constructief.#
Een vlakke golf valt van links loodrecht op een scherm dat twee gaatjes bevat (diameter \(\leq\) golflengte). De afstand tussen de gaatjes, \(d\), is bijvoorbeeld drie keer de golflengte. De vlakke golf zorgt ervoor dat de gaatjes als puntbronnen, in fase, bolvormige golven gaan uitzenden. Het licht in een punt P (zie Figuur {number}) is een superpositie van het licht dat door de twee bronnen wordt uitgezonden. We zeggen ook wel dat beide bronnen met elkaar interfereren. In Fig. 6 is de afstand die een golf aflegt van het bovenste gaatje tot P niet gelijk aan de afstand die een golf vanuit het onderste gaatje tot P aflegt. Er is een verschil in de lengte van de weg die de golven afleggen. Daardoor is de fase van de twee golven in P niet gelijk. Echter, het is mogelijk dat het faseverschil precies gelijk is aan een geheel aantal malen \(2\pi\). Het weglengteverschil is dan een geheel aantal golflengtes. In die gevallen is er sprake van constructieve interferentie en we zien een hoge lichtintensiteit in P. Deze situatie is getekend in Figuur {number}.
Opdracht 1
Het licht uit beide bronnen komt natuurlijk ook in punt M terecht.
Hoe groot is dan het weglengte (fase) verschil?
Wat betekent dat in termen van constructieve of destructieve interferentie?
Hangt dit af van de golflengte van het licht?
In Figuur {number} zien we een speciaal geval: het weglengteverschil is precies één golflengte. Het faseverschil is dan \(2\pi\) en de golven interfereren constructief in P. Voor punten die net boven of onder P liggen, is het faseverschil anders en er is geen sprake meer van \(100\%\) constructieve interferentie. De lichtintensiteit zal daardoor lager zijn. Uit Figuur {number} kun je afleiden dat het weglengteverschil goed benaderd wordt door \(d\sin \theta\) . De hoek \(\theta\) , gedefinieerd in Figuur {number}, bepaalt in wezen de ligging van P (en andersom). Constructieve interferentie treedt dus op als \(d\sin \theta = \lambda\). Er is natuurlijk ook constructieve interferentie als het weglengte (fase) verschil gelijk is aan \(m \lambda (2\pi m)\) met \(m\) een geheel getal dat we de orde van het interferentie proces noemen. Dus bij hoeken \(\theta\) die voldoen aan
zien we in de bijbehorende posities op het scherm een versterkte lichtintensiteit.
Opdracht 2
Kan \(m\) ook negatief zijn? Zo ja, wat betekent dit voor \(\theta\)? Waar ligt P dan?
Opdracht 3
Welke consequenties heeft een verandering van \(d\), \(m\) en/of \(\theta\) op de hoek waarbij er sprake is van constructieve interferentie? Welke invloed heeft een toename in \(d\) op \(m\) en \(\theta\), en welke invloed heeft een afname? En welk effect heeft een toename/afname in \(m\) op \(d\) en \(\theta\) en een toename/afname in \(\theta\) op \(m\) en \(d\)?
Interferentie in ``een punt ver weg’’: Meerdere bronnen.#
In Figuur {number} is de afstand tussen een bron en het scherm van de orde van de afstand tussen twee bronnen. Het gaat om afstanden van de orde 10 \(\mu\)m. In de praktijk kijken we niet op zo’n kleine afstand naar het licht. De afstanden waar wij mee werken liggen in het gebied 10 - 100 cm. We zijn dus geïnteresseerd in wat er gebeurt in punten die ver weg liggen van de bronnen. Voor die punten verandert Figuur {number} in het bovenste deel van Figuur {number}.
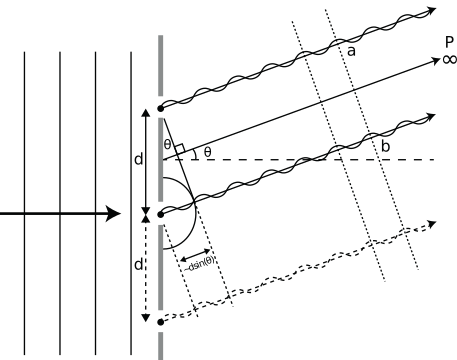
Het bovenste deel van deze figuur is identiek aan Figuur {number}, alleen ligt het punt P nu oneindig ver weg van de bronnen. In de getekende situatie is er sprake van constructieve interferentie in P. Het gedeelte van de figuur rechtsonder laat zien dat extra gaatjes op onderlinge afstand \(d\) dan ook bijdragen tot de constructieve interferentie. De schuine streepjeslijnen aan de rechterkant van de figuur kondigen de ontwikkeling van vlakke golffronten (evenwijdige bundel) aan.#
We zien dat de paden van de bronnen naar P, nu in hoge mate evenwijdig lopen. Hierdoor wordt de voorwaarde voor constructieve interferentie (vgl. ()) exact. In deze situatie is het ook niet moeilijk te bedenken wat er gebeurt als we een extra gaatje in het scherm maken. We zorgen ervoor dat het derde gaatje op de lijn ligt die door de andere twee gaatjes gaat en dat de onderlinge afstand \(d\) is (zie Figuur {number} onder). De derde bron zendt ook, in fase, een golf uit die bijdraagt tot de amplitude in het verre punt P. Het pad dat daarbij hoort, loopt parallel met de andere paden. Het weglengteverschil met de andere paden is \(\lambda\) of 2\(\lambda\). Dus de bijdrage van de derde bron interfereert constructief met die van de andere bronnen in P. Wij kunnen deze redenering voortzetten voor 4, 5, .. , \(N\) gaatjes die op een lijn liggen, met onderlinge afstand d. Op deze manier construeren we de theoretische beschrijving voor een tralie met \(N\) lijnen. De amplitude van het elektrische (magnetische) veld van het licht in P wordt dan \(N\) keer zo groot als de amplitude die teweeggebracht wordt door één gaatje.
Als we naar Figuur {number} kijken, is het verleidelijk om lijnen te tekenen die door punten met gelijke fase van de getekende golven gaan (streepjeslijnen rechts in Figuur {number}). Deze lijnen staan loodrecht op de voortplantingsrichting en je bent misschien geneigd deze lijnen als golffronten van een evenwijdige bundel op te vatten. Dat is een prima gedachte maar je moet natuurlijk wel weten of bijvoorbeeld de punten op de streepjeslijn tussen de punten a en b (in Figuur {number}) in fase trillen met de trillingen in a en b. Dichtbij de bronnen is het een ingewikkelde zaak maar ver van de bronnen is dat zeker wel zo. Je kunt dat aantonen met het principe van Huygens. Het volgt ook uit de golfvergelijking. Voor de lichtgolven die mogelijk zijn in een uniform medium staat de voortplantingsrichting altijd loodrecht op de golffronten.
Opdracht 4
In Figuur {number} is de richting van de eerste orde buiging van licht met één bepaalde golflengte getekend.
Geef de vergelijking voor de hoek voor een volgende orde grootte.
Geef van elk van de variabelen in de vergelijking aan of ze constant zijn of niet. Gebruik vgl. ().
Van transmissietralie naar reflectietralie: De tralievergelijking.#
Tot nu toe hebben we de werking van een tralie besproken aan de hand van een transmissietralie. In de praktijk wordt echter vaker een reflectietralie gebruikt. In plaats van lichtdoorlatende lijnen hebben we dan te maken met bijvoorbeeld nauwkeurige groeven. Alles wat hierboven gezegd wordt over vlakke golven, puntbronnen, etc. geldt ook voor reflectietralies. Dus ook vgl. (). Bij de afleiding van vgl. () is aangenomen dat de inkomende vlakke golf loodrecht op het tralie invalt. Die restrictie hoeft niet gemaakt te worden. De vlakke golf mag ook onder een hoek met de normaal van het tralie invallen. In Figuur {number} wordt geschetst hoe we voor een evenwijdige bundel die onder hoek \(i\) met de normaal van het tralie invalt, de hoeken \(u\) van de uitgaande bundels kunnen vinden.
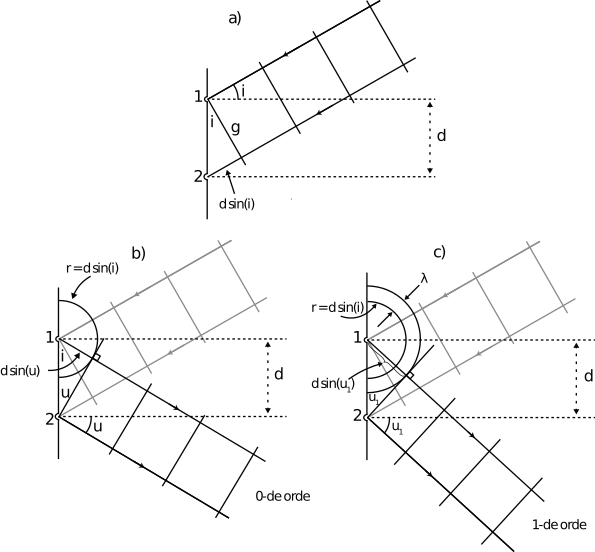
Constructie van de hoek van uitval voor een reflectietralie. a) een vlakke golf valt onder een hoek \(i\) op een tralie. Het golffront g bereikt juist tralielijn 1. Dit brengt de ontwikkeling van een bolvormig golffront vanuit 1 tot stand. Een tijdsinterval \(\Delta t =(d \sin i) / c\) later bereikt het vlakke front g tralielijn 2. b) het bolvormige golffront vanuit 1 heeft dan de straal \(d \sin i\). De trillingen op dit golffront en die in punt 2 zijn in fase. De lijn die door punt 2 gaat en die raakt aan het bolvormige golffront bepaalt de voortplantingsrichting van de 0-de orde uitgaande golffronten (golffront staat loodrecht op voortplantingsrichting) en c) de constructie van de richting van 1-de orde uitgaande bundel.#
In Figuur {number}a valt een evenwijdige bundel onder een hoek \(i\) met de normaal op het tralie. Een vlak golffront zal het eerst traliepunt 1 bereiken en volgens Huygens zendt dat punt dan bolgolven uit. Een tijd \(\Delta t\) later bereikt het golffront traliepunt 2. Uit Figuur {number}a blijkt dat \(\Delta t =(d \sin i) / c\). (\(d\) is de afstand tussen twee tralielijnen en \(c\) is de lichtsnelheid). In Figuur {number}b zien we dan hoever de bolgolf uit traliepunt 1 zich uitgebreid heeft. Zoals gezegd, de fase van punten op een golffront is per definitie gelijk, maar in dit geval heeft de trilling in traliepunt 2 ook die fase. We kunnen nu een lijn tekenen die door traliepunt 2 gaat en raakt aan de bolgolf. Deze lijn wordt loodrecht gesneden door de lijn die door traliepunt 1 gaat en het raakpunt. Deze twee lijnen kunnen gezien worden als de “voorlopers” een golffront / voortplantingsrichting paar voor de uitgaande golf (zoals besproken bij Figuur {number}). Net als in Figuur {number} kunnen we meer tralielijnen toevoegen aan de beschouwing. Figuur {number}b is bijzonder in de zin dat uit de figuur blijkt dat \(d \sin u = d \sin i\). In dit geval wordt de uitgaande bundel de 0-de orde diffractiebundel genoemd. Natuurlijk heeft niet alleen het getekende golffront in Figuur {number}b dezelfde fase als de fase in traliepunt 2. Ook golffronten die horen bij eerder vertrokken bolgolven hebben dezelfde fase (afgezien van een verschil van \(2\pi n\) natuurlijk). In Figuur {number}c zie je een bundel ontstaan uit het tekenen van de raaklijn aan het golffront met straal \((d \sin i)+ \lambda\). Uit de figuur blijkt dat in dit geval \(d \sin u_1 = (d \sin i)+ \lambda\) We kunnen dit natuurlijk ook doen voor golffronten met straal \((d \sin i)+ m\lambda\) waarbij \(m\) een geheel getal is. Voor een ingaande hoek \(i\) kunnen we de hoeken \(u_m\) van mogelijke uitgaande bundels bepalen uit:
Dit is de tralievergelijking. Wij zien hieruit direct dat, als een vlakke golf (evenwijdige bundel) met een bepaalde golflengte onder een hoek \(i\) op het tralie valt, er verschillende vlakke golven met dezelfde golflengte onder verschillende hoeken \(u_m\) worden teruggekaatst. Wij kunnen de golflengte van een bepaalde component meten door nauwkeurig \(i\) en \(u_m\) op te meten en vgl. () te gebruiken.
Opdracht 5
\(m\) kan ook negatief zijn. Wat zegt dit over de relatie tussen de hoeken \(i\) en \(u_m\)?
Het verwerken en genereren van licht met vlakke golffronten#
We kunnen proberen de richting van een evenwijdige bundel die van het tralie komt, direct te meten maar erg nauwkeurig gaat dat niet. Veel beter gaat het als we de bundel op een positieve lens laten vallen. De bundel convergeert dan tot een punt in het brandvlak. Zie Figuur {number}.
Door in het brandvlak een scherm te plaatsen, kunnen we uit de positie van de spot op het scherm de richting van de bundel bepalen. De relatie tussen de richting van de bundel en de positie op het scherm, is weergegeven in Figuur {number} rechts.
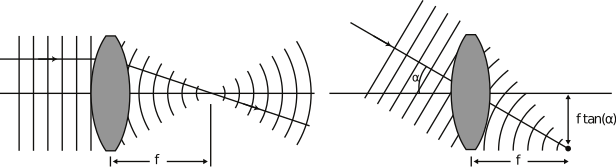
Verloop van de golffronten bij de focussering van een licht met een vlak golffront. Rechts is de relatie tussen de richting van de bundel en de positie van het brandpunt weergeven.#
Invallende lichtbundel. Optisch systeem#
Bij de afleiding van vgl. () gaan we ervan uit dat het invallende licht bestaat uit een evenwijdige bundel. Die aanname is niet gerechtvaardigd voor de lampen op het practicum. Het licht van de kwik- of de natriumlamp is divergerend van aard. We moeten het licht uit die bronnen daarom collimeren. Collimeren is eenvoudig voor een puntbron. Je hoeft de puntbron alleen maar in het brandpunt van een convergerende lens te zetten. In feite het omgekeerde van wat er gebeurt in Figuur {number}. Helaas, in ons experiment kunnen we de lampen niet opvatten als puntbronnen. Om dit op eenvoudige wijze toch enigszins voor elkaar te krijgen, maken we gebruik van een smalle spleet die in het brandpunt van een lens wordt gezet. Zie Figuur {number}.
Hoe smaller de spleet, des te beter het licht uit de lens gekenmerkt kan worden als één vlakke golf met één scherpe richting. Nadeel is natuurlijk dat de intensiteit van het licht dat op het tralie valt steeds kleiner wordt.
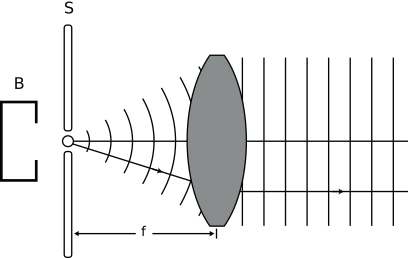
Generatie van een lichtbundel met een vlak golffront (collimatie). Het licht uit B valt door een spleet S op een convergerende lens die zo geplaatst is dat het brandpunt samenvalt met S.#
Onze opstelling om met het tralie de golflengte van spectraallijnen te meten, bestaat nu achtereenvolgens uit: een bron (lamp), een spleet, een collimerende lens, het tralie, een afbeeldinglens en een scherm. Deze onderdelen worden in feite zo opgesteld dat er een afbeelding van de spleet op het scherm wordt gemaakt. Als je bedenkt dat er een evenwijdige lichtbundel naar het tralie toegaat en dat er een evenwijdige bundel van het tralie afkomt.
Opdracht 7
Bij welk onderdeel van II-7 ben je deze manier van afbeelden tegen gekomen? Wat bepaalt of de spleet vergroot of verkleind wordt afgebeeld? Wat is gunstig om de golflengte van een spectraallijn zo nauwkeurig mogelijk te bepalen: een vergroting of een verkleining? Leg uit.
Meetmethode#
Opstelling#
De opstelling die we gebruiken voor het bepalen van de golflengte van de zichtbare spectraallijnen van de Hg en de Na lamp is weergegeven in Figuur {number}. Deze opstelling wordt wel de monochromator opstelling genoemd. Het enige onderdeel dat beweegt in deze opstelling is het tralie. Het tralie wordt gemonteerd op een draaitafel met een gradenverdeling die het mogelijk maakt de draaihoek op te meten (zie Figuur {number}).
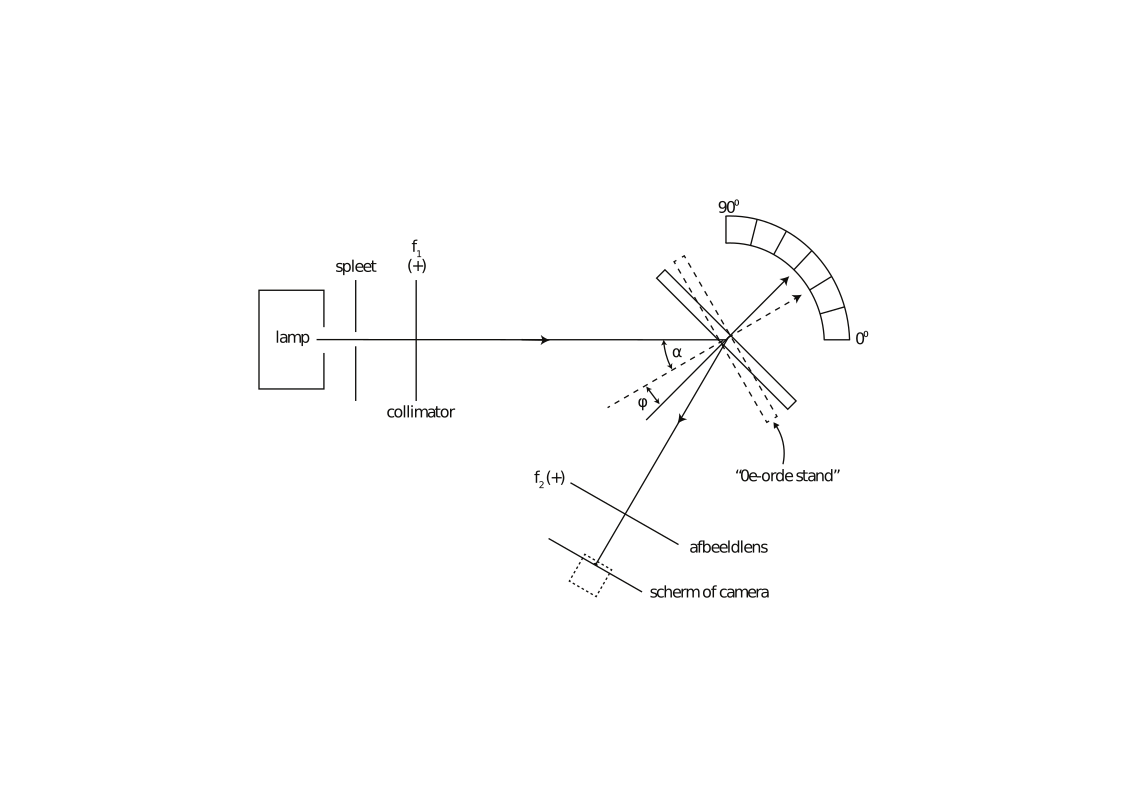
Opstelling voor het meten van de golflengte van spectraallijnen.#
De lamp, de spleet en de lens \(f_1\) genereren een gecollimeerde (evenwijdige) lichtbundel. Deze bundel valt op het tralie. We hebben gezien dat de buiging van het licht door het tralie ervoor zorgt dat, afhankelijk van de golflengte, er evenwijdige bundels onder verschillende hoeken worden teruggekaatst. Door de hoek van het tralie ten opzichte van de invallende bundel te veranderen, kunnen we licht met een bepaalde kleur met de lens \(f_2\) op een vast punt op het scherm of op de camera laten vallen. Uit de bijbehorende hoek kunnen we dan de golflengte van het licht berekenen. Er is een speciale hoek voor het tralie. Bij die hoek is het net alsof het licht door een gewone spiegel (via de lens \(f_2\)) in het vaste punt op het scherm wordt afgebeeld. In feite wordt dan het 0-de orde buigingspatroon in het vaste punt afgebeeld. De golflengte van het licht speelt hierbij geen rol. In Fig. 11 is deze stand van het tralie aangegeven met de streepjeslijn. In die stand is de hoek tussen de normaal op het tralie en richting van het inkomende licht \(\alpha\). (de hoek tussen de inkomende en uitgaande lichtbundel is dus \(2\alpha\). Bedenk dat \(\alpha\) wordt bepaald door de posities van de lamp, lens \(f_1\), lens \(f_2\) en het punt op het scherm. Als we in de praktijk met een bepaalde opstelling bijv. de golflengte van een aantal spectraallijnen willen meten, dan bepalen we de hoek die de normaal van het tralie maakt met de “spiegelstand”. In Fig. 11 is dit de hoek \(\phi\).
Uitwerking#
Als we de hoek van inval op het tralie \(i\) noemen en de hoek van uitval \(u\), dan geldt (zie Figuur {number})
Opdracht 8
Laat zien dat als je vgl. () invult in de tralievergelijking () dat je dan de volgende voorwaarde krijgt voor licht met de golflengte \(\lambda\) op het vaste punt terecht komt. \( 2 \cos \alpha \sin \varphi=-m N \lambda \) waarin het \(N\) het aantal lijnen per lengte eenheid is, \(\lambda\) de golflengte en \(m\) orde van de buiging. \(m\) kan positieve en negatieve waarden (en nul) aannemen.
Opdracht 9
Voor de situatie geschetst in Figuur {number}, is \(m\) dan positief of negatief? Klopt dat met je antwoord bij vraag 5?
Opdracht 10
Met de vergelijking uit opdracht 8 kunnen we uit metingen van \(\alpha\) en \(\phi\), \(\lambda\) bepalen. Als we de onzekerheden in \(\alpha\) en \(\phi\), \(u(\alpha)\) en \(u(\phi)\) noemen, leid dan de doorwerkingsformule voor de onzekerheid in \(\lambda\) , \(u(\lambda)\) af.
Als het verschil in golflengte van twee spectraallijnen erg klein is, kunnen wij met het blote oog de spectraallijnen niet meer gescheiden waarnemen en ook kunnen we het tralie niet nauwkeurig genoeg draaien.
Om het kleine golflengteverschil toch te kunnen meten, vervangen we het scherm door de camera. De vergroting van de camera stelt ons in staat splitsing van de spectraallijnen duidelijk waar te nemen en op te meten.
De procedure hiervoor werkt als volgt. Uit de tralievergelijking () volgt dat bij een vaste hoek van inval \(i\) een kleine verandering van de golflengte \(\lambda\) gepaard gaat met een kleine verandering in de hoek van uitval \(u\). Het verband is als volgt:
\(\Delta u\) berekenen we uit de afstand van de spectraallijnen op de camera en de brandpuntsafstand van \(f_2\). De eenheid van \(\Delta u\) is radialen.
Opdracht 11
Met vgl. () kan uit metingen van \(u\) en \(\Delta u\), \(\Delta\lambda\) bepaald worden. Je wilt natuurlijk de onzekerheid in \(\Delta\lambda\) weten. Als je op de gebruikelijke manier de doorwerkingformule gaat uitrekenen, stuit je op een notatieprobleem. Noem daarom in deze vraag de uitgaande hoek \(v\) (was \(u\)) en het kleine verschil in uitgaande hoek \(\Delta v\) (was \(\Delta u\)). Als we de onzekerheden in \(v\) en \(\Delta v\) aangeven met \(u(v)\) en \(u(\Delta v)\), leid dan de doorwerkingsformule voor de onzekerheid in \(\Delta\lambda\), \(u(\Delta\lambda)\) af.
Oplossend (scheidend) vermogen#
Spectraallijnen hebben een zekere breedte. Het is duidelijk dat als de afstand tussen twee spectraallijnen op het scherm vergelijkbaar wordt met de breedte van een lijn, dat we de twee lijnen dan niet meer goed kunnen onderscheiden. De intensiteitverdeling van het licht als functie van golflengte (of positie op het scherm) ziet er dan ongeveer uit zoals in Figuur {number}.
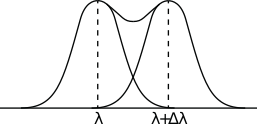
Lichtintensiteitverdeling voor twee naburige spectraallijnen. De lijnen kunnen gescheiden worden waargenomen als er sprake is van een duidelijke dip in de verdeling.#
Het oplossend (scheidend) vermogen (resolving power) van onze opstelling wordt gekarakteriseerd door de grootheid \(R\):
waarbij \(\Delta \lambda\) het minimale golflengteverschil is van twee spectraallijnen die we net kunnen onderscheiden. Vgl. () geldt voor de eerste orde. Voor hogere ordes verwachten we dat twee naburige spectraallijnen verder ”uit elkaar getrokken” worden en dat het oplossend vermogen voor hogere ordes dus groter is. In de praktijk maken we op grond van een foto van twee naburige spectraallijnen een schatting van \(\Delta\lambda\). We gebruiken dit getal en de gemiddelde waarde van de golflengtes om een praktische waarde voor het oplossend vermogen van onze opstelling te berekenen.
De theoretische bovengrens voor het oplossend vermogen van een tralie wordt gegeven door:
waarin \(m\) de orde van de spectraallijnen is. \(N_{tot}\) is het totaal aantal tralielijnen dat meedoet in het interferentie proces. Dus voor een tralie dat volledig belicht wordt, is \(N_{tot}\) het aantal lijnen op het tralie (zie ook Wolfson hfdst. 32.3).
Opdracht 12
Bedenk tenminste twee redenen waarom in de praktijk het waargenomen oplossend vermogen kleiner is dan de theoretische waarde.
Opdrachten#
Allereerst
HOUD DE TRALIES ALLEEN VAST AAN DE RECHTHOEKIGE TRALIEBEHUIZING OF AAN DE STEEL VAN DE BEHUIZING. Een vingerafdruk of een kras kan niet worden gereinigd of gerepareerd. Tralies zijn erg duur.
De spectrale lampen worden heet wanneer ze worden ingeschakeld. Houd alleen de steel van de lamp vast. Je kunt je anders lelijk branden.
Houd de lenzen en alle andere optische componenten vast aan de steel van de behuizing.
Zorg ervoor dat alle componenten, nadat je ze geplaatst hebt, stevig met de klem en schroef zijn vastgezet op het breadboard.
Nogmaals: Raak de lenzen en tralies niet aan in het centrale gedeelte.
Laat apparatuur niet los op de rand van de tafel staan. Zet ze vast. Dingen kunnen op de grond vallen en breken.
Laat geen componenten op de tafel liggen. Daarmee voorkom je beschadiging.
Kijk niet direct in de lamp. Het kan je ogen beschadigen.
Zet de lamp, camera en computer uit wanneer je ze niet gebruikt.
**Een tip: Bij het opzetten van de experimenten moet je ervoor zorgen dat het gehele optische systeem op één lijn ligt. Zorg ervoor dat elementen die op een rechte lijn moeten liggen ook echt op een rechte lijn liggen. Kijk van boven en maak gebruik van de lijnen op het breadboard. Zorg er ook voor dat alle elementen op de goede hoogte staan. Kijk van opzij en gebruik de hoogte indicator.
Hg-lamp. Aan het werk:
Bouw de monochromatoropstelling. Gebruik de Hg lamp en het 600 lijnen per mm tralie. Start met het scherm. Houd voldoende ruimte om het scherm door de camera te kunnen vervangen. Controleer de collimatie en verzeker jezelf er van dat het scherm in het brandpunt van \(f_{2}\) staat.
Draai het tralie zo dat \(i(=\alpha + \phi) = 0\). (Gebruik autocollimatie, vraag de assistent). Lees de gradenschaal af. Dit is het nulpunt voor de hoekmeting. Wijs een vast punt op het scherm aan en draai het tralie nu zo dat de 0-de orde precies op dat punt valt. Hoe herken je hier de 0-de orde? Lees de gradenschaal af en bepaal \(\alpha\). Vergeet niet een schatting van de fout in de hoeken te maken. Speel met de breedte van de spleet.
Draai nu systematisch het tralie en noteer voor iedere spectraallijn die op het gekozen punt op het scherm valt de hoek. Doe dit voor zoveel mogelijk ordes. Maak een werktabel met als koppen: kleur, orde, aflezing, \(\phi\) , \(\lambda\) en \(u(\lambda)\). Gebruik de vergelijking uit opdracht 8 en het resultaat van voorbereidingsvraag 10. Hoe kom je aan \(\phi\)? De laatste drie kolommen vergen dus wat Python werk.
Maak een plot waarbij je in een figuur verticaal de berekende golflengtes met fout plot voor iedere orde m (horizontaal). Plot in de dezelfde figuur de literatuurwaarden als horizontale streepjeslijnen.
Bereken het gewogen gemiddelde van de golflengte van iedere gemeten spectraallijn en bereken de fout in deze gemiddelde waarde. Neem als gewicht \(w = 1/u(\lambda)^2\). Gebruik hiervoor de formules die in de Appendix zijn gegeven. Is het resultaat strijdig met de literatuurwaarden?
We onderzoeken nu de splitsing van de gele Hg-lijnen. Vervang het scherm door de camera. Beeld een orde van de gele lijnen af op de camera (Opm. : de kleur op het scherm kan anders zijn. Let goed op.). (Denk aan de breedte van de spleet en het gebruik van het filter). Save het resultaat voor het verslag. (Gebruik de save icon midden boven.) Bepaal op het computerscherm de afstand tussen de lijnen uitgedrukt in pixels (knopje meetlat links in het scherm). Bereken hieruit het verschil in de hoek van uitval \(\Delta u\). Check of je waarde voor \(u\) nog actueel is. Bereken met vgl. () het verschil in golflengte \(\Delta \lambda\). Wat is de fout \(u(\Delta\lambda)\) ?
Na-lamp. Aan het werk:
Bouw de monochromatoropstelling. Gebruik de Na lamp en het 600 lijnen per mm tralie. Start met het scherm. Houd voldoende ruimte om het scherm door de camera te kunnen vervangen. Controleer de collimatie en verzeker jezelf er van dat het scherm in het brandpunt van \(f_{2}\) staat.
Draai het tralie zo dat \(i(=\alpha + \phi) = 0\). (Gebruik autocollimatie, vraag de assistent). Lees de gradenschaal af. Dit is het nulpunt voor de hoekmeting. Wijs een vast punt op het scherm aan en draai het tralie nu zo dat de 0-de orde precies op dat punt valt. Hoe herken je hier de 0-de orde? Lees de gradenschaal af en bepaal \(\alpha\). Vergeet niet een schatting van de fout in de hoeken te maken. Speel met de breedte van de spleet.
Draai nu systematisch het tralie en noteer voor iedere spectraallijn die op het gekozen punt op het scherm valt de hoek. Doe dit voor zoveel mogelijk ordes. Maak een werktabel met als koppen: orde, aflezing, \(\phi\) , \(\lambda\) en \(u(\lambda)\). Gebruik de vergelijking uit opdracht 8 en het resultaat van voorbereidingsvraag 10. Hoe kom je aan \(\phi\)? De laatste drie kolommen vergen dus wat Python werk.
Maak een plot waarbij je in een figuur verticaal de berekende golflengtes met fout plot voor iedere orde m (horizontaal). Plot in de dezelfde figuur de literatuurwaarden als horizontale streepjeslijnen. Zie je duidelijke onderlinge verschillen, wijs de ordes dan opnieuw toe.
We onderzoeken nu de splitsing van de gele Na-lijnen. Vervang het scherm door de camera. Beeld een orde van de gele lijnen af op de camera (Opm. : de kleur op het scherm kan anders zijn. Let goed op.). (Denk aan de breedte van de spleet en het gebruik van het filter). Save het resultaat voor het verslag. (Gebruik de save icon midden boven.) Bepaal op het computerscherm de afstand tussen de lijnen uitgedrukt in pixels (knopje meetlat links in het scherm). Bereken hieruit het verschil in de hoek van uitval \(\Delta u\). Check of je waarde voor \(u\) nog actueel is. Bereken met vgl. () het verschil in golflengte \(\Delta \lambda\). Wat is de fout \(u(\Delta\lambda)\) ?
Appendix#
Voor het berekenen van het gewogen gemiddelde moet je eerst een bepaald gewicht (weight) geven aan elke datapunt. Dit gebeurd met de volgende formule:
Als je naar de formule kijkt zie je dat meetpunten met een hoge onzekerheid een kleiner gewicht hebben. Dit betekent dat ze minder belangrijk zijn vergeleken met datapunten die een kleine onzekerheid hebben. Om de uiteindelijke waarde voor \(\lambda\) te vinden gebruiken we:
De uiteindelijke onzekerheid is:
Note: Deze manier van een gewogen gemiddelde is niet alleen voor dit experiment van toepassing, maar werkt altijd wanneer je een gemiddelde moet vinden en je onzekerheden hebt (dan verander je \(\lambda\) met je een andere meting). Het is in principe hetzelfde als een constante waarde fitten.
Golflengtes#
Groepsnummer |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
Element |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
1 |
2000.0 |
1000.0 |
500.00 |
250.00 |
125.00 |
62.50 |
31.25 |
15.63 |
7.81 |
3.91 |
2 |
1781.8 |
890.90 |
445.45 |
222.72 |
111.36 |
55.68 |
27.84 |
13.92 |
6.96 |
3.48 |
3 |
1587.4 |
793.70 |
396.85 |
198.43 |
99.21 |
49.61 |
24.80 |
12.40 |
6.20 |
3.10 |
4 |
1414.2 |
707.11 |
353.55 |
176.78 |
88.39 |
44.19 |
22.10 |
11.05 |
5.52 |
2.76 |
5 |
1259.9 |
629.96 |
314.98 |
157.49 |
78.75 |
39.37 |
19.69 |
9.84 |
4.92 |
2.46 |
6 |
1122.4 |
561.23 |
280.62 |
140.31 |
70.15 |
35.08 |
17.54 |
8.77 |
4.38 |
2.19 |
