Microscopie#
Bijdrage geleverd door dr. Silvania Pereira en dr. Hylkje Geertsema.
In deze beschrijving van de proef wordt geen achtergrondinformatie gegeven. Voor je op het practicum komt, word je geacht de volgende hoofdstukken uit ``Essential University Physics’’ van Richard Wolfson zeer aandachtig gelezen te hebben:
Hoofdstuk 30 : Reflection and Refraction
Hoofdstuk 31 : Images and Optical Instruments
Introductie#
Recente grote wetenschappelijke doorbraken in de biologie zijn mogelijk gemaakt door optimalisatie en verbetering van natuurkundige instrumenten. Dat heeft geleid tot diverse onderzoeksgebieden waaronder imaging physics en nanobiologie. Beide groepen zijn op de TU Delft te vinden. Imaging (ImPhys) richt zich onder andere op medische beeldvorming en het verbeteren van de huidige microscopen. Recentelijk onderzoek richt zich bijvoorbeeld op superresolutie microscopie.
De basis voor microscopie ligt bij lenzen, of misschien wel het oog. Wat kunnen we eigenlijk zelf al zien?
De dunne lenzen wet#
Een van de simpelste optische instrumenten is een dunne lens, een lens waarvan de diameter veel groter is dan de dikte van de lens. Dunne convex lenzen kunnen lichtstralen convergeren, zodat een reeel beeld wordt gevormd welke kan worden gedetecteerd met een camera. Om een scherp beeld te krijgen op de camera, moet de voorwerpsafstand en beeldafstand dusdanig gekozen worden dat ze aan de volgende formule voldoen:
Hierin is \(f\) de brandpuntsafstand van de lens in m, \(b\) de beeldsafstand in m (de afstand tussen de lens en de scherpe afbeelding daarvan), en \(v\) de voorwerpsafstand in m (de afstand tussen het voorwerp en de lens).
De sterkte van de lens kan snel en eenvoudig bepaald worden door een scherpe afbeelding van een TL buis aan het plafond af te beelden op de tafel. Doordat de beeldsafstand groot is, geldt \(\frac{1}{v} \approx 0\) en daarmee \(b \approx f\).
De afbeelding die we maken kan anders zijn van grootte dan die van het voorwerp. Voor de vergroting geldt:
hierin zijn \(V\) en \(B\) respectievelijk de grootte van het voorwerp en beeld (Ga zelf na welke voorwaarde er voor \(v\) geldt voor een vergroting!)
Afbeelden#
In ons oog zit ook een lens en wordt er een beeld geprojecteerd. Dit is schematisch weergegeven in Figuur {number}. Met onze ogen kunnen we beelden verkrijgen van voorwerpen die zich zowel ver weg als dichtbij bevinden. Wanneer de ogen ontspannen zijn, worden objecten op oneindig scherp gesteld op het netvlies. Om voorwerpen dichtbij scherp te kunnen stellen (tot op een afstand van ongeveer 25 cm), past het oog zich aan, d.w.z. het verkort de brandpuntsafstand van zijn lens. Het beeld van een voorwerp met hoogte \(V\) op een afstand \(v\) van het oog wordt bij benadering gegeven door:
De beeldgrootte \(B\) is het grootst wanneer de voorwerpsafstand is teruggebracht tot de kleinste afstand van ongeveer 25 cm. Een verdere vergroting van de beeldgrootte is alleen mogelijk met behulp van een optisch instrument dat een beeld produceert dat een grotere hoek met het oog maakt, zoals we hierna zullen zien.
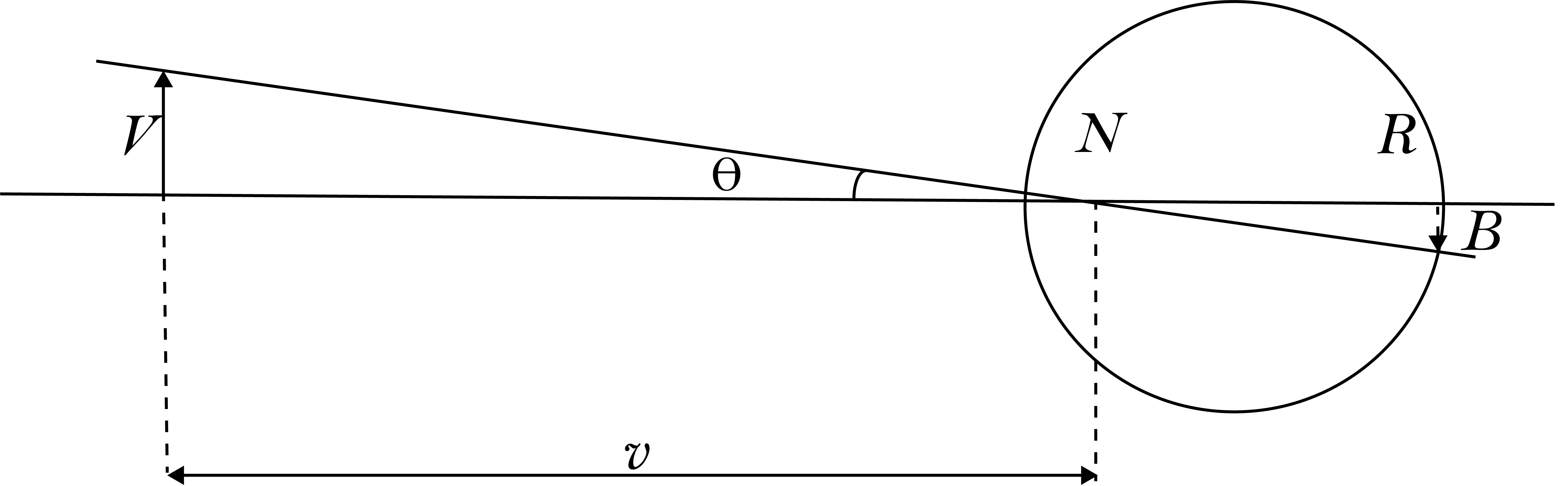
Het afbeelden in een oog#
Loep#
Een vergrootglas kan worden beschouwd als een zeer eenvoudige microscoop, omdat de hoek die het voorwerp met het oog maakt groter is en men het voorwerp met meer details kan aflezen dan met het blote oog. In Figuur {number} wordt het schema van de beeldvorming op positie \(i\) met de oog/vergrootglas combinatie getoond. Voor een voorwerp met hoogte \(h\) op \(o\) zoals in Figuur {number}, wordt de hoek \(\theta\) die het beeld bij het oog ondergaat, gegeven door:
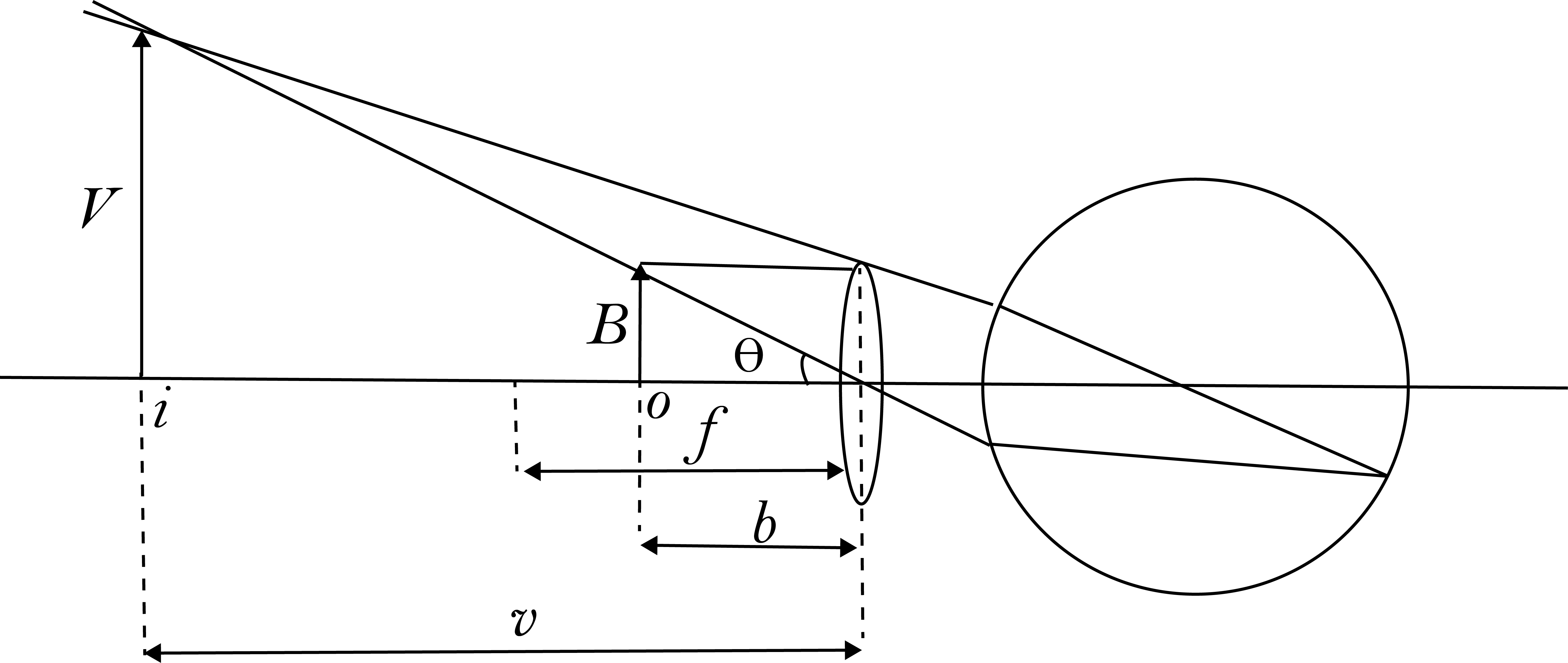
Een schematische weergave van het afbeelden met een loep#
Camera & Microscoop#
De dunne lenzen wet kun je nagaan met een camera door een scherpe afbeelding te maken bij verschillende voorwerpsafstanden. Echter weet je niet precies waar de CCD-chip zit die het licht omzet in een elektrisch signaal. Voor het bevestigen van de lenzenwet moet je dus gebruik maken van een referentiestelsel waarbij je gebruik maakt van een systematische fout in \(b\), waarbij de systematische fout de afstand is tussen je gekozen referentiepunt en je CCD-chip.
Om een vergroting scherp af te beelden heb je vaak twee lenzen nodig. Het stralendiagram van een vergroting zoals gebruikt bij een microscoop is afgebeeld in Figuur {number}. Het volstaat hier om alleen de figuur te geven, te theoretische afleiding is eenvoudig zelf uit te voeren, waarbij je zult vinden dat de vergroting gegeven wordt door:
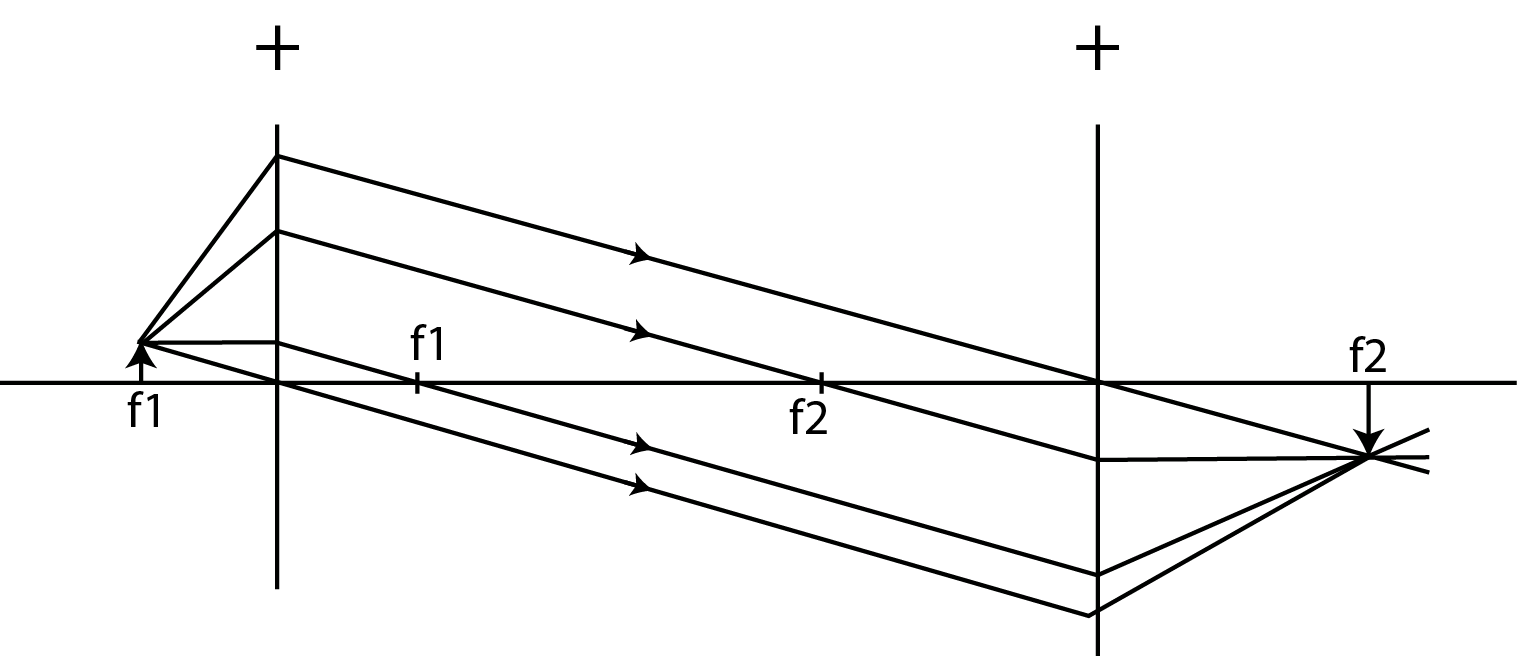
Stralendiagram van een microscoop. Het voorwerp wordt in het brandpunt van de eerste lens geplaatst. De lichtbundel in het gebied tussen de lenzen is evenwijdig en het beeld wordt gevormd bij de brandpuntafstand van de tweede lens.#
USAF 1951 testpatroon#
In dit experiment wil je natuurlijk kijken hoe goed je vergroting is die je hebt vergkregen. Het USAF 1951 testpatroon (zie Figuur {number}) wordt gebruikt om optische systemen te testen (denk bijvoorbeeld aan vergroting of resolutie). Het bestaat uit speciale sets horizontale en verticale lijnen met zeer goed gedefinieerde afmetingen en afstanden. Het patroon bestaat uit groepen en iedere groep heeft zes elementen. Het patroon herhaalt zich in het centrum naar steeds kleinere afmetingen. Voor het practicum is het USAF 1951 testpatroon op een dia beschikbaar. Voor het grootste patroon dat we met het blote oog op de dia kunnen zien, is \(G = 0\).
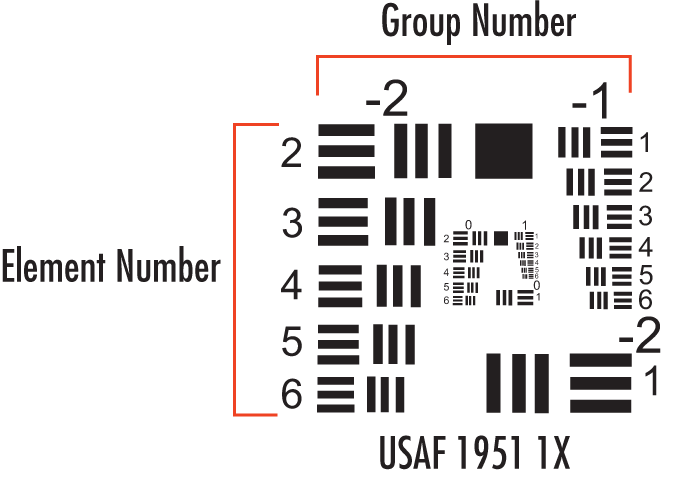
USAF1951 testpatroon. Iedere groep bestaat uit zes elementen. Bij uitvergroting komt in het centrum van het patroon steeds een fijner patroon te voorschijn. De breedte van een lijn is gelijk aan de afstand tussen de lijnen. De breedte van een lijn uit een bepaald element uit een bepaalde groep is weergegeven in tabel {number}.#
Groepsnummer |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
Element |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
1 |
2000.0 |
1000.0 |
500.00 |
250.00 |
125.00 |
62.50 |
31.25 |
15.63 |
7.81 |
3.91 |
2 |
1781.8 |
890.90 |
445.45 |
222.72 |
111.36 |
55.68 |
27.84 |
13.92 |
6.96 |
3.48 |
3 |
1587.4 |
793.70 |
396.85 |
198.43 |
99.21 |
49.61 |
24.80 |
12.40 |
6.20 |
3.10 |
4 |
1414.2 |
707.11 |
353.55 |
176.78 |
88.39 |
44.19 |
22.10 |
11.05 |
5.52 |
2.76 |
5 |
1259.9 |
629.96 |
314.98 |
157.49 |
78.75 |
39.37 |
19.69 |
9.84 |
4.92 |
2.46 |
6 |
1122.4 |
561.23 |
280.62 |
140.31 |
70.15 |
35.08 |
17.54 |
8.77 |
4.38 |
2.19 |
Brownian Motion#
Een mogelijk onderzoek met een microscoop is het bepalen van de beweging van kleine deeltjes. In ons dagelijks leven wordt ons lichaam gebombardeerd door miljoenen moleculen. Nu beïnvloedt dat onszelf niet zo veel, maar voor kleine deeltjes zorgen deze botsingen met andere moleculen voor een richtingsverandering (impulsoverdracht). Deze richtingsverandering is totaal random, waardoor de kleine deeltjes zich als ongeleide projectielen bewegen. Dit proces heet diffusie en de gemiddelde gekwadrateerde afstand die een deeltje aflegt in 2 dimensies over een bepaalde tijd, wordt gegeven door de formule:
met \(r_N\) de verplaatsingsafstand van een deeltje, \(D\) de diffusieconstante in m\(^2\)s\(^{-1}\)en \(t\) de tijd in s. Als we kijken naar meerdere deeltjes, dan verspreidt de populatie van deeltjes zich over de tijd over een steeds groter gebied. De snelheid waarmee deze spreiding plaatsvindt kan worden weergegeven met de diffusie constante \(D\) welke gegeven wordt door:
hierin is \(k_B\) de constante van Boltzmann in J/K, \(T\) de temperatuur in K, \(\eta\) de viscositeit (stroperigheid) van de vloeistof in Pa s, en \(R\) de radius van het deeltje. Door de deeltjes te tracken als functie van de tijd kun je de diffusiecoefficient bepalen.
Bronnen#
Apparatuur#
Optisch breadboard
Bevestigingen
Klemmen
Lenzen met brandpuntafstand (in mm): 10, 50 (2x), 100 (2x), 200 en 500.
Meetlint
Dia
LED lamp
Tafellamp
Microscoop dia
Diffractie preparaat
Beschrijving voor het bouwen van een microscoop met je eigen telefoon
Handleiding van Thorlabs
Diverse preparaten
