Elektromagnetisme

Inleiding

In de ontwikkelingsexperimenten heb je gewerkt met elektronica. In het Boltzmann experiment heb je gekeken naar een spanningsdeler, eigenschappen van een diode in het niet geleidende gebied, en gewerkt met digitale multimeters. Bij het RC-experiment heb je eigenschappen van een RC-circuit onderzocht. En verder heb je gekeken naar de eigenschappen van een LED. Maar er is veel meer… bij het vak Elektriciteit en Magnetisme heb je al een aantal elektronische componenten voorbij zien komen. Bij het tweedejaarsvak Elektronische Instrumentatie zal je er nog veel meer zien.

In dit experiment krijg je de kans om eigenschappen van zulke circuits te bestuderen en bijvoorbeeld je eigen AM-radio te bouwen, of verder onderzoek doen naar filters.

Basisvergelijkingen

Serieschakeling van spoel, condensator en weerstand

Om een eigen onderzoek op te zetten is het van belang dat je de verschijnselen die optreden in een serieschakeling van een spoel, condensator en weerstand aangesloten op een wisselspanningsbron, goed begrijpt. We geven daarom hier een gedetailleerde, recht toe, recht aan beschrijving van de theorie zonder gebruik te maken van phasors of complexe getallen.

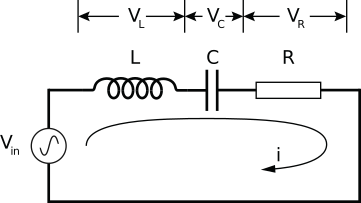
Serieschakeling van een spoel, condensator en een weerstand aangedreven door een wisselspanningsbron.

Een schematische weergave van de schakeling waarin de drie componenten zijn gebruikt is weergeven in Figuur {number}. De componenten zijn in serie geschakeld. Bij een serieschakeling loopt door alle elementen dezelfde stroom, \(i(t)\). Ons doel is, om als functie van frequentie (en amplitude) van de ingangsspanning, deze stroom uit te rekenen. We noemen de spanningen over de spoel, de condensator en de weerstand respectievelijk \(V_L\), \(V_C\) en \(V_R\). Voor deze grootheden geldt (zie Wolfson hoofdstuk 24-29 [Essential University Physics])

\[ V_L=L\frac{di}{dt} \]

\[ V_c=\frac{Q}{C}=\frac{\int i dt}{C} \]

\[ V_R=iR \]

\(L\) is de zelfinductie van de spoel, \(C\) is de capaciteit van de condensator en \(R\) is de weerstand. Voor de serieschakeling in Figuur {number} geldt dan (kringregel Kirchhoff, Wolfson hoofdstuk 25.3):

()\[ V_{i n}=L \frac{d i}{d t}+\frac{\int i dt}{C}+i R \]

Deze uitdrukking is een differentiaalvergelijking die geldt voor ingangsspanningen met een willekeurige vorm. Wij maken uitsluitend gebruik van wisselspanningen die worden beschreven door \(V_{in}(t) = V_{in}^0 sin(\omega t)\) (\(V_{in}^0\) is de amplitude, \(\omega=2\pi f\) is de hoekfrequentie en \(f\) de frequentie). In de stationaire toestand (dus niet direct na het aanschakelen van de spanningsbron) zal de stroom ook sinusvormig met de tijd veranderen. Op grond van wat we weten over faseverschillen tussen de spanning en stroom bij een enkele spoel of condensator, zit het er dik in dat de stroom \(i\) een faseverschil \(\phi\) heeft ten opzichte van \(V_{in}\). De stroom heeft dan de vorm: \(i(t)=i_0 sin(\omega t + \phi)\). \(i_0\) en \(\phi\) zijn de grootheden die we nu willen berekenen. We vullen \(V_{in}\) en \(i\) in vergelijking (). Na de differentiatie en integratie krijgen we:

()\[ V_{in}^0 \sin({\omega t}) = i_0 \boxed{\omega L} \cos({\omega t + \varphi}) - i_0 \boxed{\frac{1}{\omega C}}\cos({\omega t+\varphi}) + i_0 R\sin({\omega t+\varphi}) \]

De tegengestelde tekens van de eerste twee termen in deze vergelijking betekenen dat in de de schakeling de spanning over de spoel (gedeeltelijk) gecompenseerd wordt door de spanning over de condensator (en omgekeerd).

Resonantiecircuits

Een bijzondere situatie treedt op als:

()\[ i_0 \omega L = \frac{i_0}{\omega C} \]

Er is in dit geval sprake van volledige compensatie en vergelijking () wordt

\[ V_{i n}^{0} \sin \omega t=i_{0} R \sin (\omega t+\varphi) \]

Dit geldt voor alle \(t\) alleen als:

()\[ i_{0}=\frac{U_{i n}^{0}}{R} \quad \text { en } \quad \varphi=0 \]

De spanning over de weerstand is in deze bijzondere situatie dus gelijk aan de spanning die de bron afgeeft. De amplitude van de stroom is gelijk aan de amplitude van de spanningsbron gedeeld door \(R\). Dit betekent dat de wisselstroom in fase is met \(V_{in}\).

De amplitude van de spanning over de condensator wordt gegeven door,

()\[ V_C^0 = \frac{i_0}{\omega C} = \frac{1}{\omega C R}V_{in}^0 \]

We zien dat als \(\frac{1}{\omega C} \gg R\) de spanning over de condensator veel groter kan worden dan \(V_{in}^0\)!

De bijzondere situatie () noemen we resonantie. Als \(L\) en \(C\) een vaste waarde hebben dan treedt resonantie op bij de hoekfrequentie \(\omega_r\) :

\[ \omega_{r}^{2}=\frac{1}{L C} \text { of in frequentie } f_{r}=\frac{1}{2 \pi \sqrt{L C}} \]

\(f_r\) wordt de resonantiefrequentie genoemd.

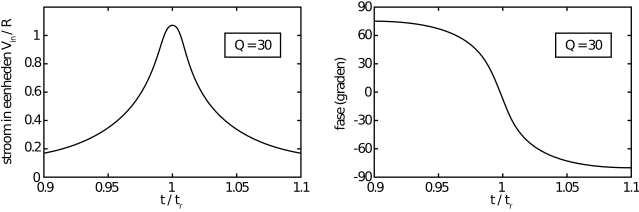
links: Amplitude van de stroom in een serie-LCR schakeling als functie van de frequentie. \(f_r\) is de resonantiefrequentie; rechts: het faseverschil tussen de stroom en de ingangsspanning als functie van de frequentie.

Parallelschakeling van spoel, condensator en weerstand

Op basis van de wetten van Kirchhoff kunnen we een soortgelijke afleiding doen voor een circuit waarbij alle elektrische componenten parallel geschakeld zijn (in zo’n schakeling moeten we er wel voor oppassen dat er een wisselspanning aangeboden wordt of dat er een weerstand in serie met de spoel wordt geplaatst).

Een van de interessante eigenschappen van deze schakeling, is dat als de bronspanning wegvalt (uitgezet wordt), de condensator zich ontlaadt over de spoel, maar door de eigenschappen van de spoel (zelfinductie) de condensator ook weer opgeladen wordt. Er ontstaat dus een wisselspanning met afnemende amplitude (bedenk waarom). Nou daaraan verbonden (en aan de resonantiecircuit) is de Q-factor.

De Q-factor

Een praktische vraag: Stel we hebben een serie-LCR schakeling werkend bij de resonantiefrequentie. Hoe snel valt dan de stroom af als we de frequentie verhogen of verlagen? Of: hoe scherp is de resonantie? Vaak wordt een relatieve grootheid gebruikt om de scherpte van de resonantie te karakteriseren, namelijk de kwaliteitsfactor Q. Een definitie van Q is:

()\[ Q=\frac{f_{r}}{B}\left(=\frac{1}{\omega_{r} C R}=\frac{\omega_{r} L}{R}\right) \]

Resonantie is belangrijk om een signaal goed te kunnen versturen. Een hoge \(Q\)-factor gunstig is voor een grote uitgangsspanning. Een ander voordeel is natuurlijk dat een hoge \(Q\) ook een smalle bandbreedte impliceert. Als er meerdere zenders in de lucht zijn met frequenties die dicht bij elkaar liggen, dan biedt een smalle bandbreedte ons de mogelijkheid alleen die frequentie er uit te pikken waar we in geïnteresseerd zijn. Dit doen we door de resonantiefrequentie met de variabele condensator af te stemmen op deze interessante frequentie. Signalen die in frequentie meer schelen dan de bandbreedte worden sterk verzwakt. Hoe kleiner de bandbreedte is, hoe beter dat dat gaat. We noemen dit selectiviteit.

Je kunt in dit onderzoek proberen een signaal te versturen met behulp van een spoel. Het magneetveld dat we met de gebruikte spoelen kunnen opwekken, waaiert echter nogal uit. Dit uitgewaaierde veld kunnen we op enige afstand detecteren door te kijken welke spanning dat veld in een andere spoel induceert. Hoge frequenties zijn gunstig voor dit proces (denk aan inductiespanning). Wij willen echter informatie met frequenties lager dan, zeg, 20 kHz overbrengen. We lossen dit probleem op door een hoogfrequent signaal te gebruiken waarvan de amplitude instantaan het laagfrequente signaal volgt. Het hoogfrequente signaal wordt wel een draaggolf genoemd. Het meegeven van het laagfrequente signaal in de amplitude van het hoogfrequente signaal noemen we amplitude modulatie. Het principe is ter verduidelijking in Figuur {number} links weergegeven.

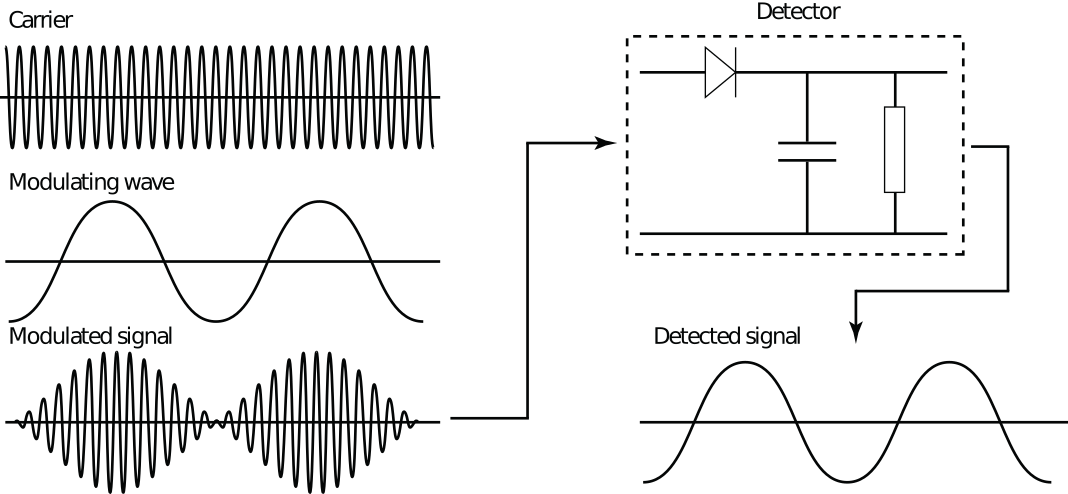
Principe van amplitude modulatie en demodulatie.

We zien dat de amplitude van de hoogfrequente draaggolf bepaald wordt door een signaal met een veel lagere frequentie. Het modulerende signaal kan weer terug verkregen worden door gebruik te maken van een diode (zie Fig {number} rechts). De werking van deze schakeling wordt besproken in hoofdstuk 28.6, p.502 van Wolfson. In het bovenstaande voorbeeld is sprake van 100% modulatie. De amplitude van het hoogfrequente signaal wordt nul als de modulerende golf minimaal is. We zeggen dat de modulatiediepte 100% is. 0% modulatiediepte correspondeert met een ongemoduleerde draaggolf. We zullen zien dat er een reden is om niet altijd voor 100% modulatie te kiezen.

Materialen

In het experiment heb je de beschikking over een functiegenerator, een oscilloscoop, instelbare weerstanden, instelbare condensatoren, verschillende spoelen. Daarnaast kun je gebruik maken van coax-kabels maar ook van een probe. Verder zijn er twee oude practicumbeschrijving tot de beschikking om eigenschappen van RLC circuits verder te bestuderen en een AM radio te bouwen. LTSPice kan gebruikt worden als simulatiesoftware.