Elasticiteitsmodulus#
Een belangrijke, maar zeker ook interessante stofeigenschap is de elasticiteitsmodulus. De elasticiteitsmodulus is de verhouding tussen de spanning (\(\sigma = \frac{F}{A}\)) en rek (\(\epsilon = \frac{\Delta l}{l} \)):
In dit experiment kun je de elasticiteits modulus of Young’s modulus bepalen op basis van de doorbuiging van een staaf en op basis van mechanische resonantie. Deze laatste vorm van bepaling van de elasticiteitsmodulus is wel erg interessant omdat deze onverwacht gerelateerd is aan quantummechanische experimenten. In het Steele-lab wordt onder andere onderzoek gedaan naar de verbinding tussen de algemene relativiteitstheorie en quantummechanica. Daartoe worden ‘staafjes’ (cantilevers) met een hoge Q-factor aangedreven. Alhoewel de daadwerkelijke experimenten te complex zijn voor het eerstejaarsnatuurkunde practicum, kunnen we de basis van deze experimenten wel begrijpen door de mechanische resonantie van een staaf te onderzoeken.
Bepaling op basis van statische buiging#
In dit experiment belast je een metalen lat waardoor deze doorbuigt. De buiging kun je nauwkeurig bepalen met behulp van een metallisch rekstrookje (Figuur 1) en de brug van Wheatstone. In een rekstrookje zorgt een lengte verandering \(\Delta l\) voor een weerstandsverandering \(\Delta R\) door:
De K-factor (gauge factor) wordt door de fabriek opgegeven. De waarde van K ligt voor de meeste type rekstrookjes tussen 2 en 4.5 en is over een groot gebied temperatuurongevoelig en onafhankelijk van de rek.
Voor de rek \(\epsilon\) aan de bovenzijde op afstand \(x\) van het belastingpunt geldt:
hierin is \(F\) de belastende kracht, \(b\) de breedte van de staaf, \(h\) de hoogte van de staaf en \(E\) de elasticiteitsmodulus van het staafmateriaal. Omdat het rekstrookje op de staaf is geplakt, volgt uit de relatieve weerstandsverandering direct de rek:
Om de relatieve weerstandsverandering nauwkeurig te bepalen, maken we gebruik van de brug van Wheatstone (zie onderdeel algemene meettechnieken). Deze schakeling is afgebeeld in Figuur {number}. In de schakeling wordt er gebruik gemaakt van een 10 slags glijweerstand met een maximale weerstandswaarde van 1.15 \(\Omega\) en een tolerantie van 10%. Elke omwenteling bestaat uit 100 schaaldelen waardoor een weerstandsverandering van 10\(^{-3} \Omega\) mogelijk is.
Met de substitutie:
is af te leiden dat geldt:
waarbij \(R_i\) de initiele waarde van \(R_2+R_{glij}\) is om het spanningsverschil op 0 te stellen (de brug in evenwicht te brengen). \(\Delta R_{glij}\) is de weerstandsverandering van de glijweerstand. Hieruit kan dan vervolgens de elasticiteitmodulus worden bepaald.
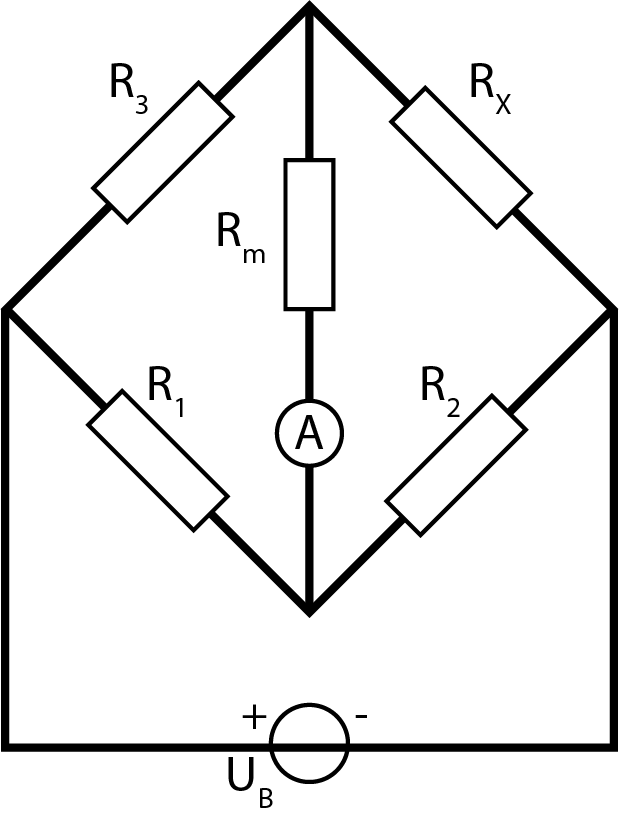
De brug van Wheatstone maakt het mogelijk om zeer nauwkeurig weerstandsveranderingen te meten.#
Bepaling op basis van eigenfrequentie#
Een tweede methode om de elasticiteitsmodulus te bepalen is op basis van de eigenfrequentie. Hiervoor kunnen we een draad klemmen tussen twee punten en belasten. De maat van belasting wordt tot uitdrukking gebracht in de frequentie die geproduceerd wordt. Dit is simpelweg analoog aan het stemmen van bijvoorbeeld een gitaarsnaar: span je deze strakker aan, dan wordt de kracht uitgeoefend op de snaar groter en daarmee de frequentie hoger.
Op het practicum zijn daarvoor twee verschillende opstellingen, zo hebben we de opstelling van Searle (voor pianosnaren), maar ook een eigen gemaakte opstelling (voor gitaarsnaren).
De grondtoon in een snaar wordt gegeven door:
waarin de golflengte \(\lambda_0 = 2L\), met \(L\) de lengte van de snaar tussen de twee vaste punten. De voortplantingssnelheid in de snaar wordt gegeven door:
met \(\mu\) de massa per lengte-eenheid (\(m/L\)). Als we er van uitgaan dat de draad niet noemenswaardig dunner wordt bij belasting, geldt er \(F=\sigma A=E\epsilon A\), met \(E\) de elasticiteitsmodulus en \(\epsilon\) de rek (\(\epsilon=\Delta L/L\)). Wanneer we bovenstaande combineren krijgen we de uitdrukking:
Op basis van het meten van de lengte verandering en de frequentie(verandering) kunnen we dus de elasticiteitsmodulus van een gitaar/pianosnaar bepalen.
De volgende bron biedt wat informatie over verschillende gitaarsnaren en bijbehorende eigenschappen.
De stemvork#
Een stemvork is een bekend hulpmiddel om instrumenten mee te stemmen. De frequentie is 440 Hz, maar deze kan aangepast worden door een blokje op een bepaalde hoogte vast te stellen. De frequentie wordt gegeven door:
Hierin is \(f\) de frequentie in Hz, \(l\) de lengte van de ‘tanden’ in m, \(E\) de elasticiteitsmodulus in Pa s, \(I\) het oppervlaktetraagheidsmoment in m\(^4\), \(\rho\) de dichtheid in kg/m\(^3\) en \(A\) het oppervlak in m\(^2\). Met twee stemvorken kun je ook het verschijnsel van resonantie onderzoeken. Het kan ook interessant zijn om te onderzoeken hoe die frequentie afhangt van de temperatuur van de staaf.

De fysica van de stemvork is wellicht complexer dan verwacht#
Q-factor#
De kwaliteitsfactor \(Q\) is een maat voor resonantie. De Q-factor wordt ookwel de kwaliteitsfactor genoemd. Bij een gitaarsnaar geeft het grofweg aan hoe lang de snaar nog trilt nadat deze is aangeslagen. De Q-factor is gedefinieerd als de verhouding tussen de opgeslagen energie en de gedissipeerde energie per cyclus:
De Q-factor geeft een kwalitatieve beschrijving van de sterkte van demping voor eenvoudige gedempte trillingen. Daarbij worden verschillende regionen voor \(Q\) onderscheden: * \(Q < 1/2\), overdemping * \(Q = 1/2\), kritische demping * \(Q > 1/2\), onderdemping
Voor een eenvoudig massaveersysteem geldt: \(Q=\frac{\sqrt{Mk}}{D}\), waarin \(M\) de massa is, \(k\) de veerconstante en \(D\) de dempingscoefficient. Verder geldt \(F_{demping}=Dv\) waarin \(v\) de snelheid is. Maar geldt er een zelfde relatie voor een gitaarsnaar? Is er sprake van snelheidsafhankelijke demping of van structurele demping. En, hoe hangt de kwaliteitsfactor af van de rek? Zowel theoretisch als experimenteel?
Bepaling op basis van mechanische resonantie#
Een derde methode om de elasticiteitsmodulus van aluminium en andere materialen te bepalen is doormiddel van de mechanische resonantie. Een staaf die is ingeklemd, zoals weergegeven in Figuur {number}, zal het liefst willen trillen in de eigenfrequentie. Als dat gebeurt praten we over een mechanische resonator. Leggen we een (wissel)kracht \(F\) aan loodrecht op de staaf, dan zal deze oscilleren. De laagste eigenfrequentie of resonantiefrequentie van deze staaf wordt gegeven door
Waarbij \(d\) de dikte is van de staaf, \(L\) de lengte tot en met de fixatie en \(\rho\) de dichtheid. Verder is \(C_0=\frac{m_0^2}{4\pi\sqrt{3}}\) een constante met \(m_0=1.875\), volgend uit \(cosh(m_0)cos(m_0)=-1\); we vinden \(C_0=0.1616\). We geven hier de afleiding niet (deze vereist de nodige integralen), maar ook hier kan de energie aanpak worden gevolgd. Merk op dat de vorm van de uitdrukking veel lijkt op vergelijking (10)
Uitdrukking () betekent dat, als de afmetingen \(L\) en \(d\), en de specifieke massa \(\rho\) bekend zijn, de resonantiefrequentie \(f_0\) direct de Young modulus \(E\) oplevert.
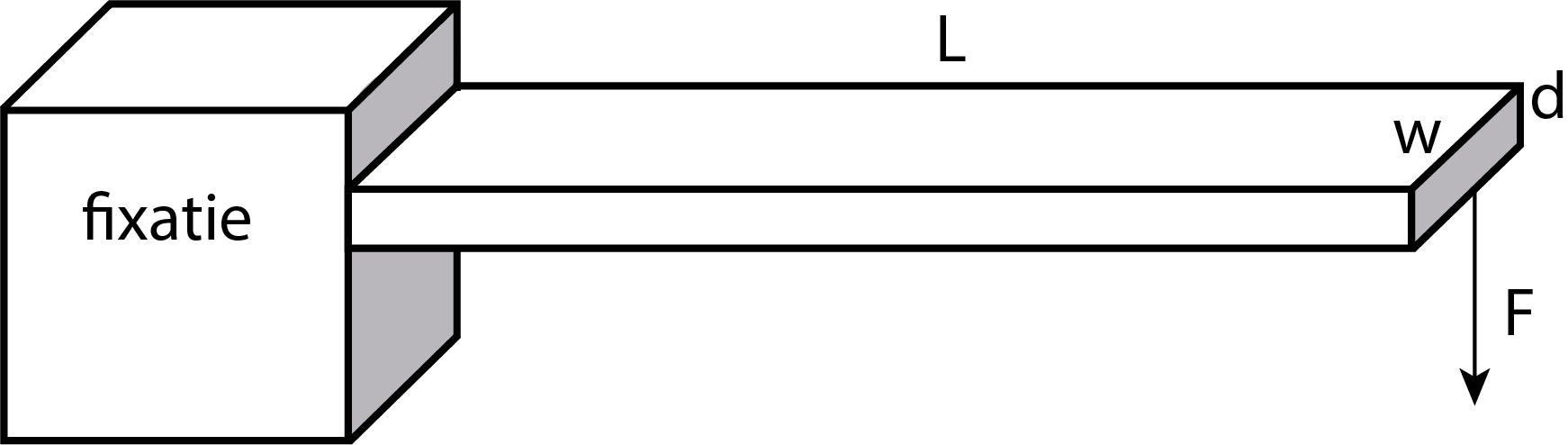
Eenzijdig ingeklemde staaf met lengte \(L\), dikte \(d\) en breedte \(w\). De aangelegde kracht \(F\) en de resulterende uitwijking staan in de richting van de dikte \(d\).#
Bij een resonantie experiment moet de staaf in trilling worden gebracht en de oscillerende beweging gedetecteerd worden (Figuur {number}). Voor de aandrijving gebruiken we een in trilling gebrachte kolom lucht. De luchtkolom wordt in beweging gezet door een luidspreker aangedreven door een wisselstroom \(I_{luidsp}\cos(2\pi ft)\). Dat het mogelijk is met een luidspreker iets in trilling te brengen weet elke popconcert bezoek(st)er!
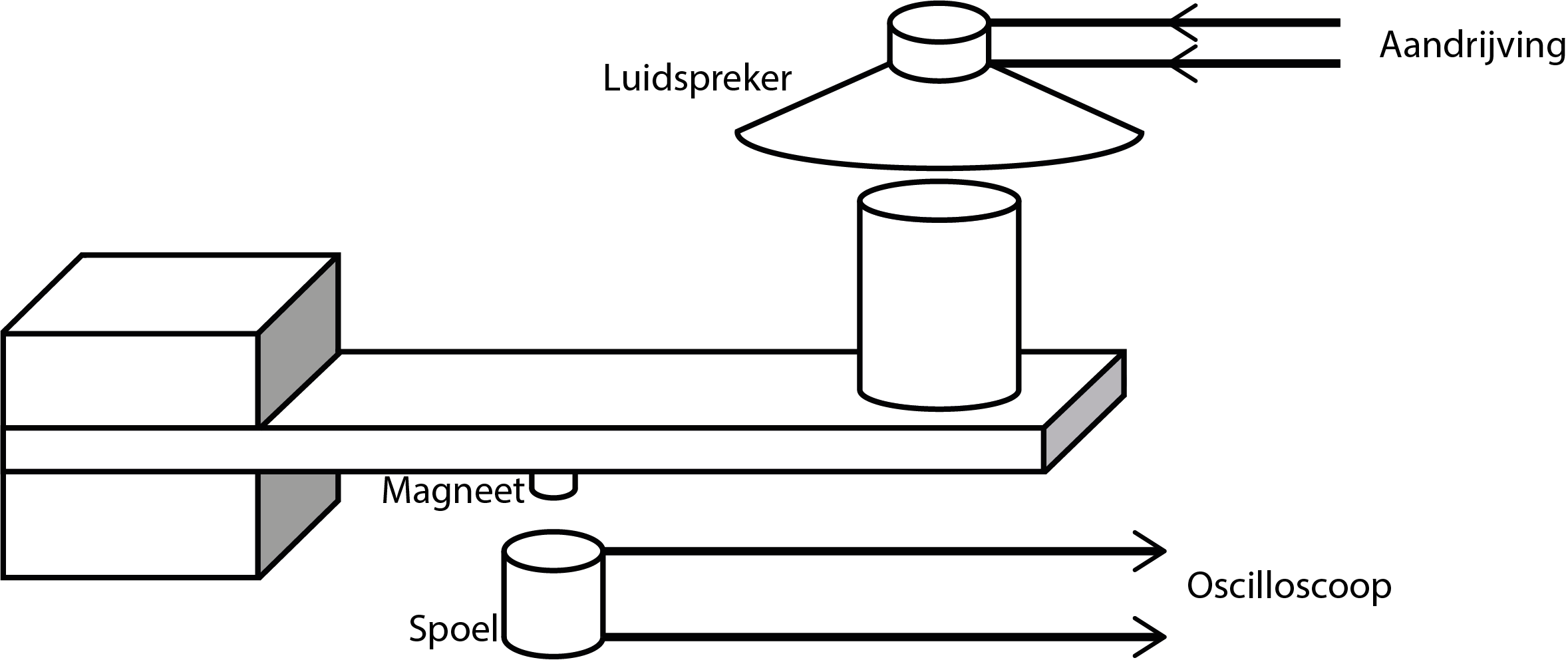
De aandrijving verloopt akoestisch door een luidspreker; de bewegingsdetectie van de ingeklemde staaf door de bewegende magneet bij een spoel.#
Op de staven die beschikbaar zijn bij het practicum is op een vaste plek een magneet bevestigd. De combinatie van deze magneet en een spoel parallel aan deze magneet (Figuur {number}) gebruiken we om de beweging van de staaf te meten. Wanneer de staaf met een frequentie \(f\) oscilleert zal de permanente magneet in de spoel een wisselende magnetische flux \(\phi(t)\) induceren met dezelfde frequentie. Deze flux levert een spanning \((V_{sp}=-\frac{d\phi}{dt})\), dus opnieuw met de frequentie \(f\) (vgl. een dynamo of een tachometer op je fiets). Deze geënduceerde wisselspanning wordt op de oscilloscoop gemeten. Bij een vaste frequentie is de amplitude van deze spanning een directe maat voor de amplitude van de uitwijking van de staaf.
Als de staaf resoneert zal de amplitude van de staaf maximaal zijn. Dus de bepaling van de maximale uitgangsspanning van de spoel levert direct de resonantiefrequentie. Deze frequentie kan met de tijdbasis van de oscilloscoop of door aflezen van de wisselstroomgenerator worden bepaald.
In het experiment zijn staven beschikbaar van messing, aluminium, plastic (PVC) en roestvast staal (RVS), en met verschillende lengtes. Het magneetje is op een vaste afstand van een van de uiteinden van de staaf gemonteerd. Een van de vele mogelijkheden met deze opstelling is het verifiëren van vgl. ().
Demping#
De amplitude van de uitwijking van de staaf is afhankelijk van het medium waarin de staaf resoneert. Bij de opstelling van de mechanische resonator (Figuur {number}) is het mogelijk om het uiteinde van de staaf meer of minder ver in een vloeistof te brengen. Hierdoor verandert de maximale uitwijking van de staaf, er treed in meer of mindere mate demping op.
Om de mate van deze demping te kwantificeren wordt de Q-factor gebruikt. Het is hierbij mogelijk om de Q-factor te relateren aan de diepte van de staaf in de vloeistof, of aan het gebruikte materiaal. Het is belangrijk je te realiseren, dat, ook als de staaf de vloeistof niet raakt, er toch al demping is, door het in rilling brengen van de lucht. Dat levert een initiële Q-factor \(Q_0\) op. De inverse van de Q-factor (\(\frac{1}{Q}\)) is een maat voor het energieverlies per oscilatie. Dit betekent dat de verschillende verliezen als volgst kunnen worden opgeteld:
met \(Q_{vl}\) de Q-factor t.g.v. de vloeistof demping. Hierbij moet eerst \(Q_0\) worden bepaald, en daarna kan de diepte-afhankelijke vloeistofbijdrage \(Q_{vl}\) worden bepaald uit de totale Q. Er kan bijvoorbeeld worden onderzocht of \(\frac{1}{Q_{vl}}\) lineair schaalt met de diepte.
Theoretische achtergrond van de niet-ideale resonator: Q-factor en resonantie-breedte#
De amplitude \(A_0\) van de uitwijking is afhankelijk van de frequentie \(f=\frac{\omega}{2 \pi}\) van de aandrijving (\(F(T)=F_0\cos(2\pi f t)\)). Hierbij geldt het volgende verband:
waarin \(b\) een dempingsparameter is, die de energiedissipatie bepaalt, \(F_0\) de maximale kracht die op de staaf wordt uigeoefened, \(m\) de massa, \(\omega\) de frequentie en \(\omega_0\) de eigenfrequentie.
Uit Wolfson 13.6, vgl. 13.17 volgt hierbij de Q-factor van een mechanische resonator:
Als de mechanische resonator in een vloeistof staat, zorgt de viscositeit van de vloeistof voor meer demping. De kracht werkend op een plaat met een zekere oppervlakte \(A\) en op een afstand \(l\) van de wand die met een snelheid \(v\) door een medium (gas of vloeistof met viscositeit \(\eta\)) beweegt, wordt gegeven door:
Vergelijken we deze uitdrukking voor de wrijvingskracht met die voor de dempingskracht in Wolfson 13.6 (\(F_d = -bv\)) dan is de dempingsfactor \(b\) direct te herkennen. Duidelijk neemt \(b\) toe met een toenemend bewegend oppervlak in de vloeistof.
Er zijn verschillende methodes om de Q-factor te bepalen. Dit zullen we uitleggen aan de hand van de resonantie curve van een mechanische resonator met een resonantiefrequentie \(f_0 = 50\) Hz (Figuur {number}).
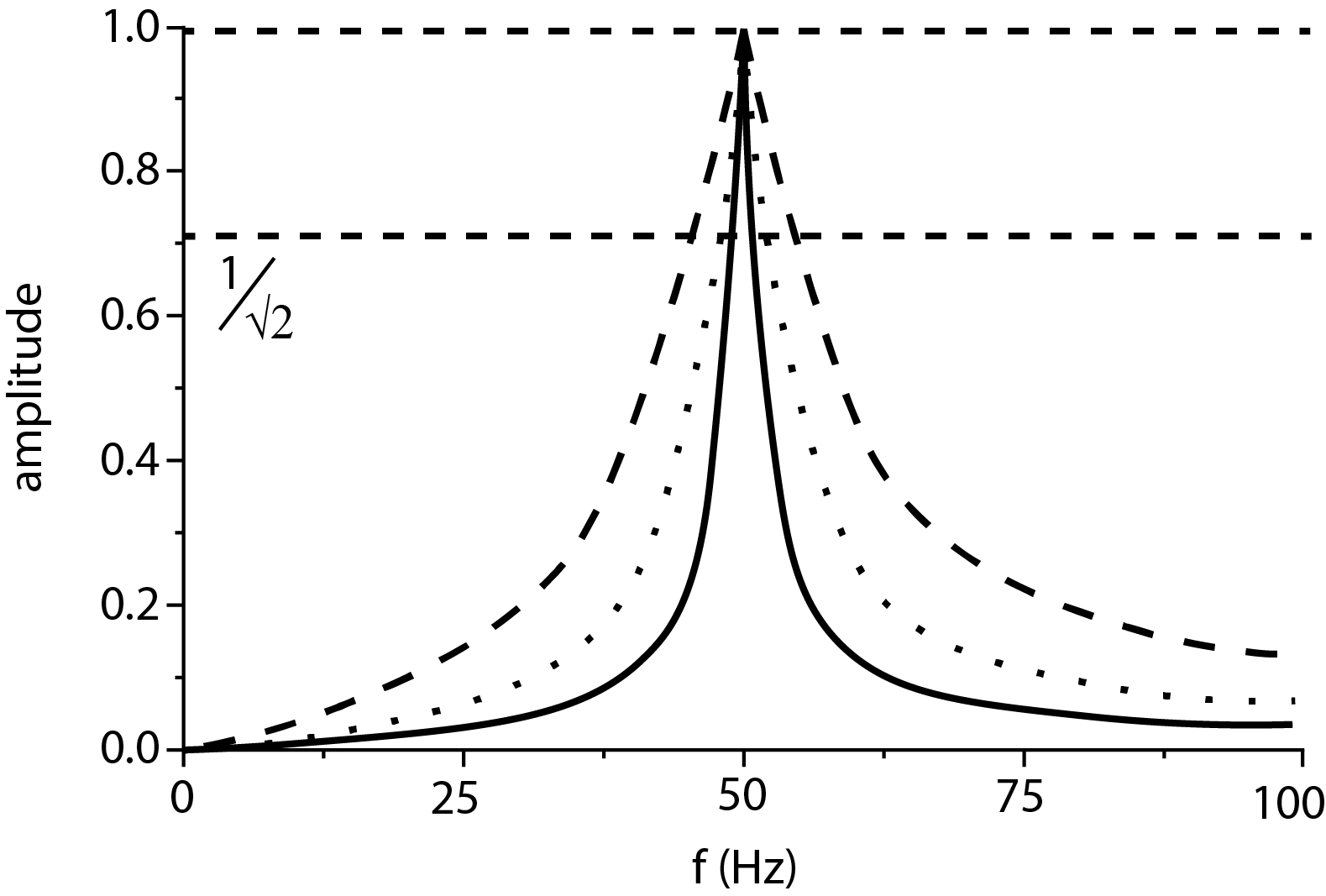
Resonantie curve van een resonator met een resonantiefrequentie \(f_0\) = 50 Hz. De amplitude heeft een scherp maximum als de frequentie f van de aandrijving overeenkomt met de resonantiefrequentie \(f_0\). De piekbreedte is afhankelijk van de demping: grote demping geeft een brede piek en dus een kleine \(Q\)-factor.#
Figuur {number} toont de vorm van de amplitude tegen de frequentie van de aangeboden aandrijving met een constante aandrijfamplitude \(F_0\). Duidelijk is de scherpe piek op de resonantiefrequentie \(f_0= \omega_0/2\pi\). Voor andere frequenties is de in de resonator opgeslagen energie kleiner. De breedte van de resonantie curve geeft een indicatie van de demping. De breedte van de piek definiëren we zo dat de opgeslagen energie bij twee frequenties \(f_l\) en \(f_h\), met \(f_l < f_0 < f_h\) (en dus \(\omega_l < \omega_0 < \omega_l\)), de helft is van die op resonantie, d.w.z. dat de amplitude \(\sqrt{2}\) maal zo klein is. Uit vgl. \ref{eq:amplitude} volgt voor de amplitude op de resonantiefrequentie
Vervolgens moeten we de frequenties berekenen waarbij \(A_{0}\left(\omega_{l}\right)=A_{0}\left(\omega_{l}\right)=A_{0}\left(\omega_{0}\right) / \sqrt{2}\). Dat vraagt wat werk, maar je vindt uiteindelijk voor het verschil \(\Delta\omega = \omega_l - \omega_h\)
Aan deze uitdrukkingen zien we dat de breedte van de resonantiepiek klein is wanneer de dissipatie klein is (d.w.z. \(b\sim0\)). Een kleine dissipatie betekent ook een grote Q-factor, en deze relatie is eenvoudig te vinden door het combineren van de vgln () en ():
Dit is de meest bekende representatie van de Q-factor: het is de inverse van de relatieve breedte van de resonantiepiek, bepaald uit de frequenties waarbij de opgeslagen energie de helft is van die bij resonantie.
De opstelling#
De literatuurwaarden van de elasticiteitsmodulus van aluminium is 70\(\cdot\)10\(^9\) N/m\(^2\).
\(K\) = 2.00 \(\pm\) 0.02.
De maximale belasting is 1.5 kg.
Oscilloscoop, digitaal, 2 kanaals, Rigol DS1102E (data opslag op USB stick mogelijk)
Sinus generator, met digitaal instelbare frequentie, Thurlby-Thandar TG55
Vermogensversterker SUB-50C, 50 W, 25 Hz-160 Hz
Bord met condensatoren (2.2, 3.3, 4.7, 6.8 en 22 μF), 2 spoelen (2.2 en 6.8 mH) en weerstanden (\(330 \Omega\), 1, 3.3, 10 en \(100\) k\(\Omega\))
Kist met daarin een luidspreker, met luchtkolomgeleider; opengewerkte demo
In hoogte instelbaar inklemsysteem met detectorspoel met BNC connector
Strips van de materialen aluminium, messing, RVS en PVC, met diverse afmetingen
Maatbekertje met glycerine (dempingsvloeistof met \(\eta = 0.950 \ \mathrm{Pa\cdot s}\))
De opstelling en materialen#
Beschikbaar is:
een gitaarsnaar opstelling met nauwkeurig verstelbare lengte
oscilloscoop met geluidsensor
verschillende snaren
stemvork
telefoon met Phyphox
boven beschreven opstellingen
Literatuur#
What gives musical instruments their sound? Acoustic Standing Waves: A Battle Between Models
